Menu Close

0-pi-4-sin-x-cos-x-3-sin-2x-dx-

Tinku Tara 0 Comments
Pin




Question Number 69735 by mhmd last updated on 27/Sep/19
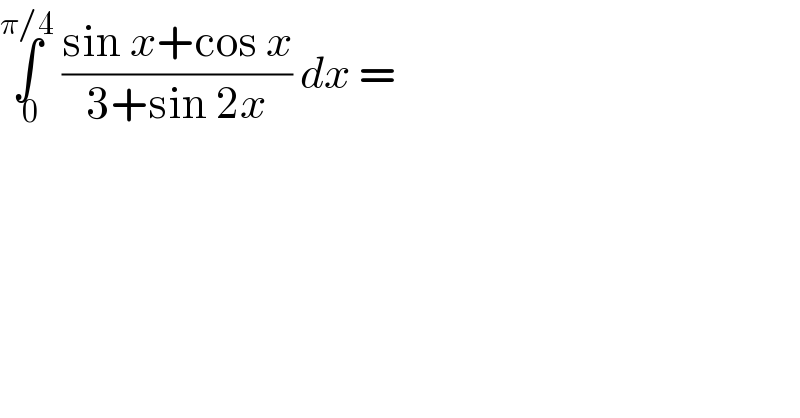
∫_( 0) ^(π/4) ((sin x+cos x)/(3+sin 2x)) dx =
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 27/Sep/19
I=∫_0 ^(π/4) ((sinx+cosx)/(3+sin(2x)))dx ⇒ I =∫_0 ^(π/4) ((sinx+cosx)/(3+2sinx cosx))dx =_(tan((x/2))=t) ∫_0 ^((√2)−1) ((((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 )))/(3+2((2t)/(1+t^2 ))×((1−t^2 )/(1+t^2 ))))((2dt)/(1+t^2 )) =∫_0 ^((√2)−1) ((2t+1−t^2 )/((1+t^2 )^2 {3+((4t(1−t^2 ))/((1+t^2 )^2 ))}))(2dt =∫_0 ^((√2)−1) ((−2t^2 +4t+2)/(3(t^2 +1)^2 +4t−4t^3 ))dt =∫_0 ^((√2)−1) ((−2t^2 +4t+2)/(3(t^4 +2t^2 +1)+4t−4t^3 ))dt = ∫_0 ^((√2)−1) ((−2t^2 +4t+2)/(3t^4 +6t^2 +3+4t−4t^3 ))dt =∫_0 ^((√2)−1) ((−2t^2 +4t+2)/(3t^4 −4t^3 +6t^2 +4t+3))dt the roots of 3t^4 −4t^3 +6t^2 +4t +3 are t_1 =1+1,4142i (complex) t_2 =1−1,4142i(complex) t_3 =−0,3333+0,4714i (complex) t_4 =−0,3333−0,4714i(complex) ⇒ F(t)=((−2t^2 +4t+2)/(3t^4 −4t^3 +6t^2 +4t+3)) =((−2t^2 +4t +2)/((t−t_1 )(t−t_1 ^− )(t−t_2 )(t−t_2 ^− ))) =((−2t^2 +4t+2)/((t^2 −2Re(t_1 )t +∣t_1 ∣^2 )(t^2 −2Re(t_2 )t +∣t_2 ∣))) =((at +b)/(t^2 −2Re(t_1 )t +∣t_1 ∣^2 )) +((bt +d)/(t^2 −2Re(t_2 )t +∣t_2 ∣^2 )) ⇒ ∫ F(t)dt =∫ ((at+b)/(t^2 −2Re(t_1 )t+∣t_1 ∣^2 ))dt +∫ ((bt+d)/(t^2 −2Re(t_2 )t +∣t_2 ∣^2 ))dt ....be continued...
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{sinx}+{cosx}}{\mathrm{3}+{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{sinx}+{cosx}}{\mathrm{3}+\mathrm{2}{sinx}\:{cosx}}{dx} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{3}+\mathrm{2}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{t}+\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left\{\mathrm{3}+\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}}\left(\mathrm{2}{dt}\right. \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{−\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} }{dt}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} }{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}{t}^{\mathrm{4}} \:+\mathrm{6}{t}^{\mathrm{2}} \:+\mathrm{3}+\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} }{dt}\:=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{−\mathrm{2}{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} \:+\mathrm{6}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{3}}{dt} \\ $$$${the}\:{roots}\:{of}\:\mathrm{3}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} \:+\mathrm{6}{t}^{\mathrm{2}} \:+\mathrm{4}{t}\:+\mathrm{3}\:{are} \\ $$$${t}_{\mathrm{1}} =\mathrm{1}+\mathrm{1},\mathrm{4142}{i}\:\:\left({complex}\right) \\ $$$${t}_{\mathrm{2}} =\mathrm{1}−\mathrm{1},\mathrm{4142}{i}\left({complex}\right) \\ $$$${t}_{\mathrm{3}} =−\mathrm{0},\mathrm{3333}+\mathrm{0},\mathrm{4714}{i}\:\left({complex}\right) \\ $$$${t}_{\mathrm{4}} =−\mathrm{0},\mathrm{3333}−\mathrm{0},\mathrm{4714}{i}\left({complex}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{2}}{\mathrm{3}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{3}} \:+\mathrm{6}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{3}}\:=\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{4}{t}\:+\mathrm{2}}{\left({t}−{t}_{\mathrm{1}} \right)\left({t}−\overset{−} {{t}}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)\left({t}−\overset{−} {{t}}_{\mathrm{2}} \right)} \\ $$$$=\frac{−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{4}{t}+\mathrm{2}}{\left({t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:\:+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{2}} \right){t}\:+\mid{t}_{\mathrm{2}} \mid\right)} \\ $$$$=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} }\:+\frac{{bt}\:+{d}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{2}} \right){t}\:+\mid{t}_{\mathrm{2}} \mid^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\int\:\:\:\frac{{at}+{b}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} }{dt}\:+\int\:\:\frac{{bt}+{d}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{2}} \right){t}\:+\mid{t}_{\mathrm{2}} \mid^{\mathrm{2}} }{dt} \\ $$$$….{be}\:{continued}… \\ $$
Answered by Kunal12588 last updated on 27/Sep/19
I=∫((sin x + cos x)/(3 + sin 2x))dx let sin x − cos x = t ⇒(sin x + cos x) dx = dt t^2 =1−2sin x cos x =1−sin 2x ⇒t^2 −4=−3−sin 2x x→0⇒t⇒−1 x→(π/4)⇒t⇒0 I=∫(dt/(2^2 −t^2 ))=(1/4)log∣((2+t)/(2−t))∣+c ∫_( 0) ^(π/4) ((sin x+cos x)/(3+sin 2x)) dx =(1/4)[log∣((2+t)/(2−t))∣]_(−1) ^0 =(1/4){0−log1+log3}=(1/4)log3
$${I}=\int\frac{{sin}\:{x}\:+\:{cos}\:{x}}{\mathrm{3}\:+\:{sin}\:\mathrm{2}{x}}{dx} \\ $$$${let}\:{sin}\:{x}\:−\:{cos}\:{x}\:=\:{t} \\ $$$$\Rightarrow\left({sin}\:{x}\:+\:{cos}\:{x}\right)\:{dx}\:=\:{dt} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{sin}\:{x}\:{cos}\:{x}\:=\mathrm{1}−{sin}\:\mathrm{2}{x} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{4}=−\mathrm{3}−{sin}\:\mathrm{2}{x} \\ $$$${x}\rightarrow\mathrm{0}\Rightarrow{t}\Rightarrow−\mathrm{1} \\ $$$${x}\rightarrow\frac{\pi}{\mathrm{4}}\Rightarrow{t}\Rightarrow\mathrm{0} \\ $$$${I}=\int\frac{{dt}}{\mathrm{2}^{\mathrm{2}} −{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}{log}\mid\frac{\mathrm{2}+{t}}{\mathrm{2}−{t}}\mid+{c} \\ $$$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{log}\mid\frac{\mathrm{2}+{t}}{\mathrm{2}−{t}}\mid\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{0}−{log}\mathrm{1}+{log}\mathrm{3}\right\}=\frac{\mathrm{1}}{\mathrm{4}}{log}\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *