Question Number 52950 by gunawan last updated on 15/Jan/19
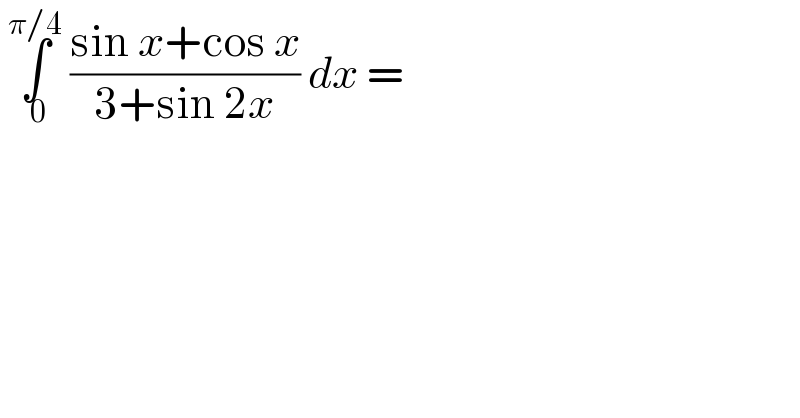
$$\:\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{3}+\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 15/Jan/19
![let A =∫_0 ^(π/4) ((sinx +cosx)/(3 +sin(2x)))dx ⇒ A =∫_0 ^(π/4) (((√2)sin(x+(π/4)))/(3+sin(2x)))dx =_(x+(π/4)=u) ∫_(π/4) ^(π/2) (((√2)sin(u))/(3+sin(2(u−(π/4)))))du =(√2)∫_(π/4) ^(π/2) ((sinu)/(3−cos(2u)))du =(√2)∫_(π/4) ^(π/2) ((sinu)/(3−(2cos^2 u−1)))du =(√2)∫_(π/4) ^(π/2) ((sinu du)/(4−2cos^2 u)) =((√2)/2) ∫_(π/4) ^(π/2) ((sinu)/(2−cos^2 u))du =_(cosu =t) ((√2)/2) ∫_((√2)/2) ^0 ((−dt)/(2−t^2 )) =((√2)/2) ∫_0 ^((√2)/2) (dt/(2−t^2 )) =((√2)/2) ∫_0 ^((√2)/2) ((1/( (√2)+t)) +(1/( (√2)−t)))dt =(1/(2(√2))) ((√2)/2) [ln∣(((√2)+t)/( (√2)−t))∣]_0 ^(1/( (√2))) =(1/4){ln∣(((√2)+(1/( (√2))))/( (√2)−(1/( (√2)))))∣}=(1/4)ln((3/1))=((ln(3))/4)](https://www.tinkutara.com/question/Q52986.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{sinx}\:+{cosx}}{\mathrm{3}\:+{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\sqrt{\mathrm{2}}{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{3}+{sin}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$=_{{x}+\frac{\pi}{\mathrm{4}}={u}} \:\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\sqrt{\mathrm{2}}{sin}\left({u}\right)}{\mathrm{3}+{sin}\left(\mathrm{2}\left({u}−\frac{\pi}{\mathrm{4}}\right)\right)}{du}\:=\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinu}}{\mathrm{3}−{cos}\left(\mathrm{2}{u}\right)}{du} \\ $$$$=\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sinu}}{\mathrm{3}−\left(\mathrm{2}{cos}^{\mathrm{2}} {u}−\mathrm{1}\right)}{du}\:=\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinu}\:{du}}{\mathrm{4}−\mathrm{2}{cos}^{\mathrm{2}} {u}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sinu}}{\mathrm{2}−{cos}^{\mathrm{2}} {u}}{du}\:=_{{cosu}\:={t}} \:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} ^{\mathrm{0}} \:\:\frac{−{dt}}{\mathrm{2}−{t}^{\mathrm{2}} }\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \:\:\:\frac{{dt}}{\mathrm{2}−{t}^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+{t}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−{t}}\right){dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\left[{ln}\mid\frac{\sqrt{\mathrm{2}}+{t}}{\:\sqrt{\mathrm{2}}−{t}}\mid\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\mid\frac{\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\:\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\mid\right\}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{3}}{\mathrm{1}}\right)=\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{4}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![∫_0 ^(π/4) ((d(sinx−cosx))/(4−1+sin2x)) ∫_0 ^(π/4) ((d(sinx−cosx))/(4−(sinx−cosx)^2 )) [formula ∫(dx/(a^2 −x^2 ))dx=(1/(2a))ln(((a+x)/(a−x)))] (1/(2×2))∣ln{((2+(sinx−cosx))/(2−(sinx−cosx)))}∣_0 ^(π/4) (1/4)[ln(((2+0)/(2−0)))−ln(((2+0−1)/(2−0+1)))] =(1/4)[0−ln1+ln3] so answer is =((ln3)/4) pls check...](https://www.tinkutara.com/question/Q52952.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{4}−\mathrm{1}+{sin}\mathrm{2}{x}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sinx}−{cosx}\right)}{\mathrm{4}−\left({sinx}−{cosx}\right)^{\mathrm{2}} }\:\:\left[{formula}\:\int\frac{{dx}}{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\left(\frac{{a}+{x}}{{a}−{x}}\right)\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}×\mathrm{2}}\mid{ln}\left\{\frac{\mathrm{2}+\left({sinx}−{cosx}\right)}{\mathrm{2}−\left({sinx}−{cosx}\right)}\right\}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\left(\frac{\mathrm{2}+\mathrm{0}}{\mathrm{2}−\mathrm{0}}\right)−{ln}\left(\frac{\mathrm{2}+\mathrm{0}−\mathrm{1}}{\mathrm{2}−\mathrm{0}+\mathrm{1}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{0}−{ln}\mathrm{1}+{ln}\mathrm{3}\right] \\ $$$${so}\:{answer}\:{is}\:=\frac{{ln}\mathrm{3}}{\mathrm{4}}\:\:{pls}\:{check}… \\ $$
Commented by gunawan last updated on 16/Jan/19

$$\mathrm{Yes}\:\mathrm{Sir},\:\mathrm{nice}\:\mathrm{solution} \\ $$
Commented by gunawan last updated on 16/Jan/19

$$\mathrm{Yes}\:\mathrm{Sir},\:\mathrm{nice}\:\mathrm{solution} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Jan/19

$${thank}\:{you}… \\ $$
