Question Number 43625 by peter frank last updated on 12/Sep/18
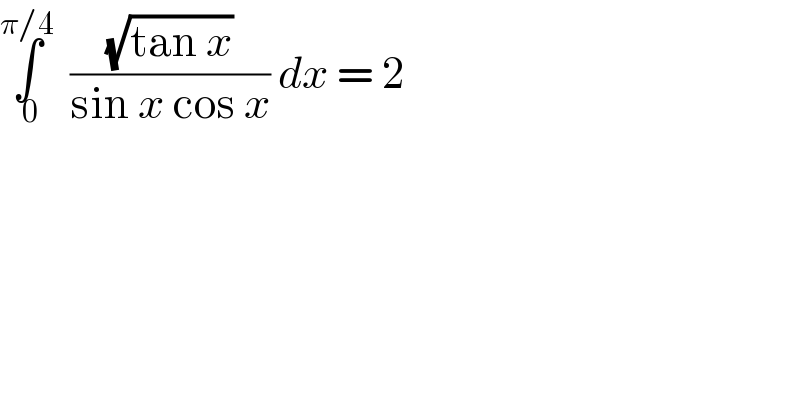
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}\:{dx}\:=\:\mathrm{2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Sep/18
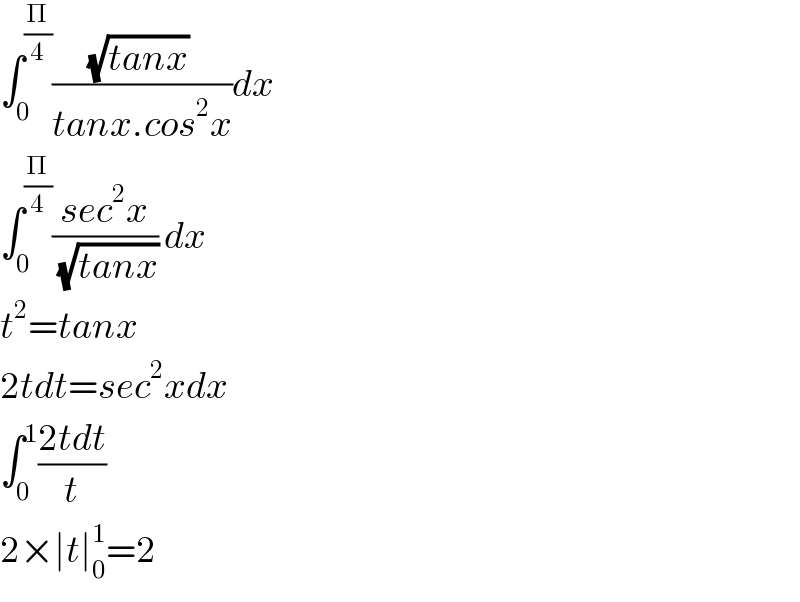
$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{\sqrt{{tanx}}\:}{{tanx}.{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} {x}}{\:\sqrt{{tanx}}}\:{dx} \\ $$$${t}^{\mathrm{2}} ={tanx} \\ $$$$\mathrm{2}{tdt}={sec}^{\mathrm{2}} {xdx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{tdt}}{{t}} \\ $$$$\mathrm{2}×\mid{t}\mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2} \\ $$
