Question Number 64335 by Chi Mes Try last updated on 16/Jul/19
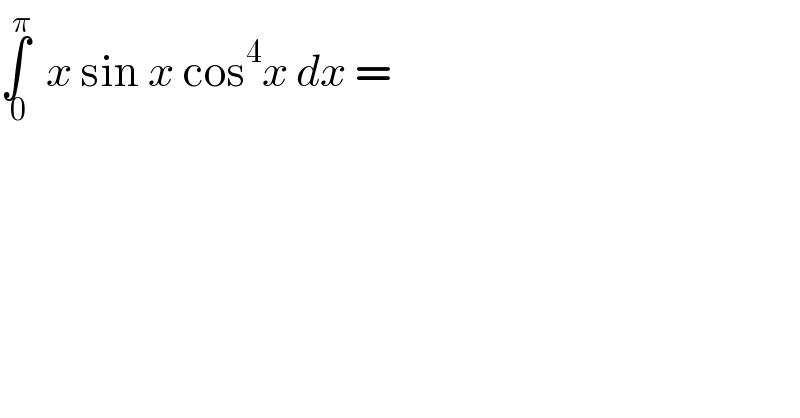
$$\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}^{\mathrm{4}} {x}\:{dx}\:= \\ $$
Answered by Tanmay chaudhury last updated on 17/Jul/19
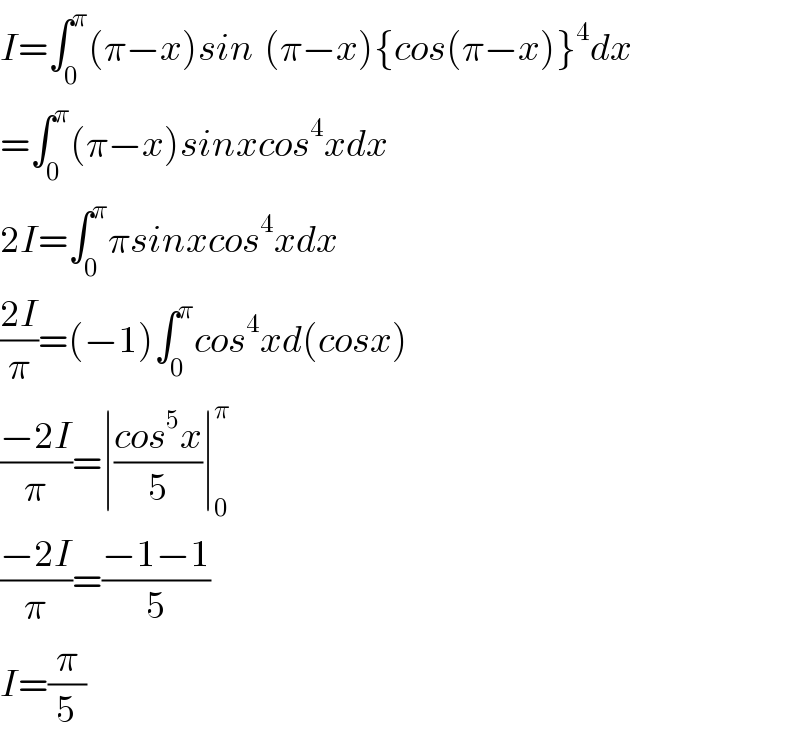
$${I}=\int_{\mathrm{0}} ^{\pi} \left(\pi−{x}\right){sin}^{} \left(\pi−{x}\right)\left\{{cos}\left(\pi−{x}\right)\right\}^{\mathrm{4}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left(\pi−{x}\right){sinxcos}^{\mathrm{4}} {xdx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \pi{sinxcos}^{\mathrm{4}} {xdx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\left(−\mathrm{1}\right)\int_{\mathrm{0}} ^{\pi} {cos}^{\mathrm{4}} {xd}\left({cosx}\right) \\ $$$$\frac{−\mathrm{2}{I}}{\pi}=\mid\frac{{cos}^{\mathrm{5}} {x}}{\mathrm{5}}\mid_{\mathrm{0}} ^{\pi} \\ $$$$\frac{−\mathrm{2}{I}}{\pi}=\frac{−\mathrm{1}−\mathrm{1}}{\mathrm{5}} \\ $$$${I}=\frac{\pi}{\mathrm{5}} \\ $$
Commented by Chi Mes Try last updated on 17/Jul/19

$${wow}\:\:{fnx}\:\:{boss}\sharp\sharp \\ $$
Commented by Tanmay chaudhury last updated on 17/Jul/19

$${thank}\:{you}\:{sir}… \\ $$
