0-x-log-x-1-x-2-2-dx-

Question Number 59049 by ugwu Kingsley last updated on 03/May/19

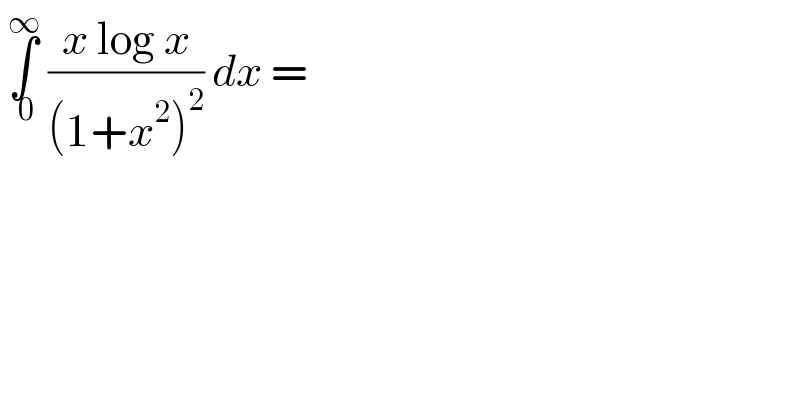
$$\:\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{x}\:\mathrm{log}\:{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:= \\ $$

Commented by maxmathsup by imad last updated on 04/May/19

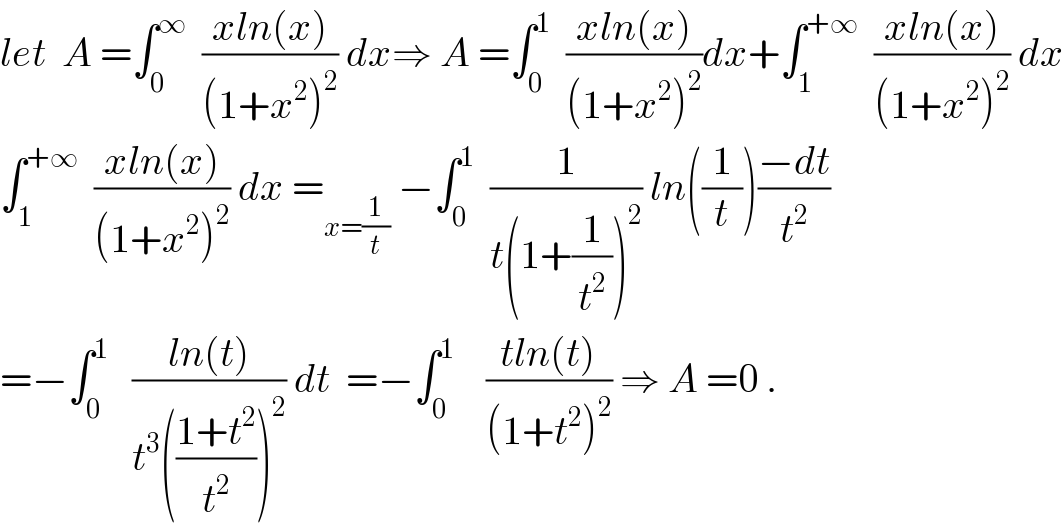
let A =∫_0 ^∞ ((xln(x))/((1+x^2 )^2 )) dx⇒ A =∫_0 ^1 ((xln(x))/((1+x^2 )^2 ))dx+∫_1 ^(+∞) ((xln(x))/((1+x^2 )^2 )) dx ∫_1 ^(+∞) ((xln(x))/((1+x^2 )^2 )) dx =_(x=(1/t)) −∫_0 ^1 (1/(t(1+(1/t^2 ))^2 )) ln((1/t))((−dt)/t^2 ) =−∫_0 ^1 ((ln(t))/(t^3 (((1+t^2 )/t^2 ))^2 )) dt =−∫_0 ^1 ((tln(t))/((1+t^2 )^2 )) ⇒ A =0 .

$${let}\:\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}+\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{xln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{xln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:=_{{x}=\frac{\mathrm{1}}{{t}}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{{t}\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{ln}\left(\frac{\mathrm{1}}{{t}}\right)\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{3}} \left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:{dt}\:\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{tln}\left({t}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow\:{A}\:=\mathrm{0}\:. \\ $$

Facebook Tweet Pin

0-x-log-x-1-x-2-2-dx-

Leave a Reply Cancel reply