Question Number 27281 by kemhoney78@gmail.com last updated on 04/Jan/18
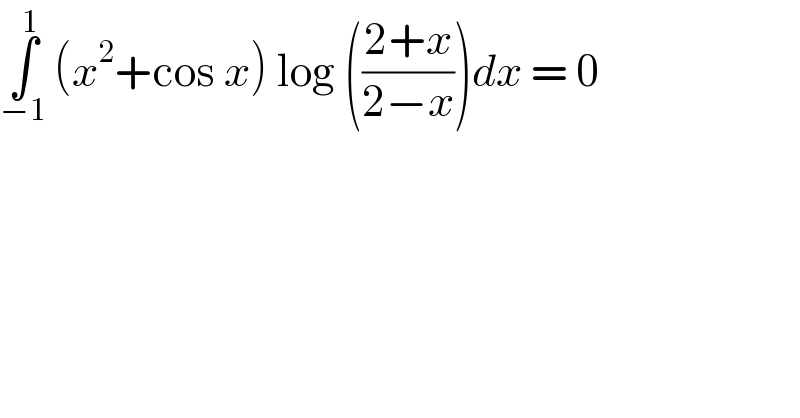
$$\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\:\left({x}^{\mathrm{2}} +\mathrm{cos}\:{x}\right)\:\mathrm{log}\:\left(\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\right){dx}\:=\:\mathrm{0} \\ $$
Commented by abdo imad last updated on 04/Jan/18
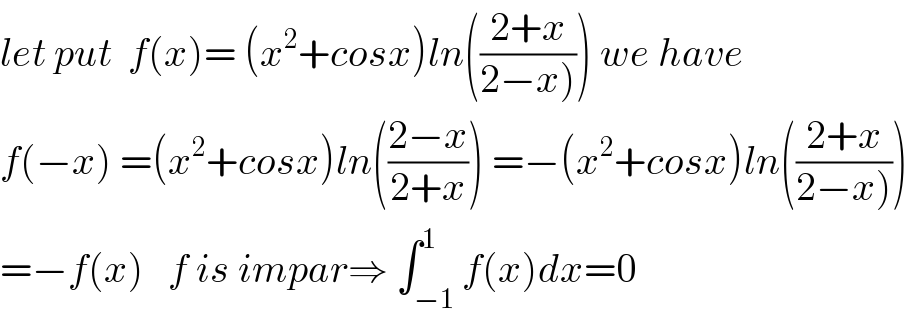
$${let}\:{put}\:\:{f}\left({x}\right)=\:\left({x}^{\mathrm{2}} +{cosx}\right){ln}\left(\frac{\mathrm{2}+{x}}{\left.\mathrm{2}−{x}\right)}\right)\:{we}\:{have} \\ $$$${f}\left(−{x}\right)\:=\left({x}^{\mathrm{2}} +{cosx}\right){ln}\left(\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}\right)\:=−\left({x}^{\mathrm{2}} +{cosx}\right){ln}\left(\frac{\mathrm{2}+{x}}{\left.\mathrm{2}−{x}\right)}\right) \\ $$$$=−{f}\left({x}\right)\:\:\:{f}\:{is}\:{impar}\Rightarrow\:\int_{−\mathrm{1}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$
Answered by ajfour last updated on 04/Jan/18
![I=∫_(−1) ^( 1) (x^2 +cos x)log (((2+x)/(2−x)))dx =∫_(−1) ^( 1) (x^2 +cos x)log (((2−x)/(2+x)))dx using ∫_a ^( b) f(x)dx=∫_a ^( b) f(a+b−x)dx 2I=∫_(−1) ^( 1) (x^2 +cos x)[log (((2+x)/(2−x)))+log (((2−x)/(2+x)))]dx 2I=0 ⇒ I=0 .](https://www.tinkutara.com/question/Q27284.png)
$${I}=\int_{−\mathrm{1}} ^{\:\:\mathrm{1}} \left({x}^{\mathrm{2}} +\mathrm{cos}\:{x}\right)\mathrm{log}\:\left(\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\right){dx} \\ $$$$\:\:=\int_{−\mathrm{1}} ^{\:\:\mathrm{1}} \left({x}^{\mathrm{2}} +\mathrm{cos}\:{x}\right)\mathrm{log}\:\left(\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}\right){dx} \\ $$$${using}\:\int_{{a}} ^{\:\:{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{\:\:{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$$\mathrm{2}{I}=\int_{−\mathrm{1}} ^{\:\:\mathrm{1}} \left({x}^{\mathrm{2}} +\mathrm{cos}\:{x}\right)\left[\mathrm{log}\:\left(\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}\right)+\mathrm{log}\:\left(\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}\right)\right]{dx} \\ $$$$\mathrm{2}{I}=\mathrm{0}\:\:\Rightarrow\:\:{I}=\mathrm{0}\:. \\ $$
