Question Number 55774 by gunawan last updated on 04/Mar/19
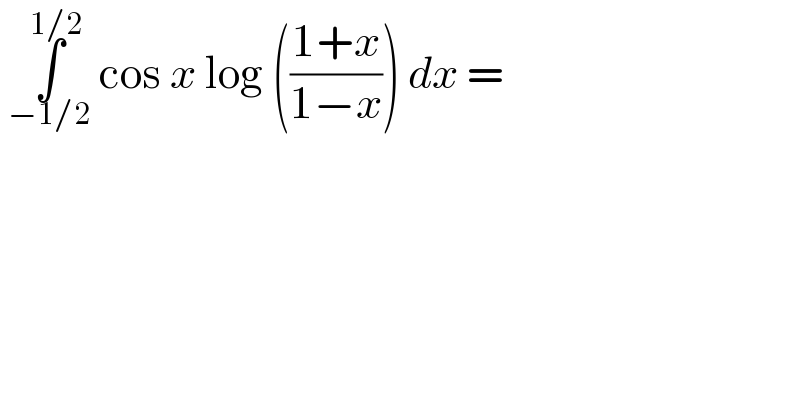
$$\:\underset{−\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\:\mathrm{cos}\:{x}\:\mathrm{log}\:\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)\:{dx}\:= \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Mar/19
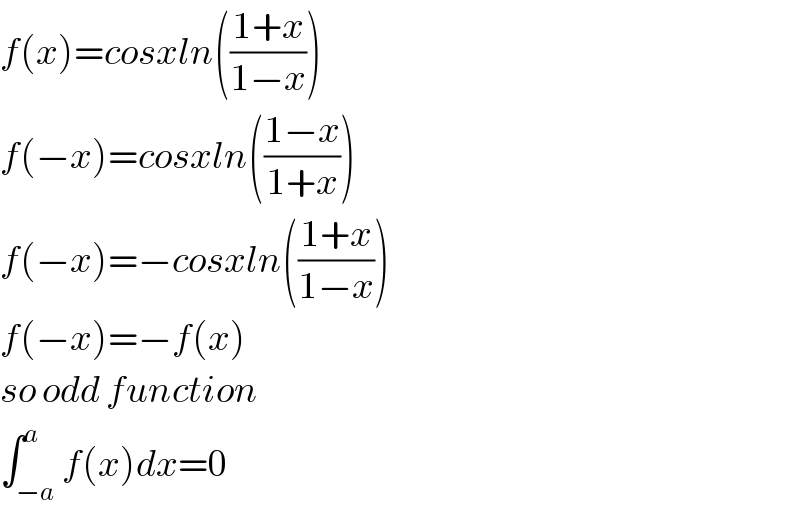
$${f}\left({x}\right)={cosxln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$${f}\left(−{x}\right)={cosxln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right) \\ $$$${f}\left(−{x}\right)=−{cosxln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$${f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$$${so}\:{odd}\:{function} \\ $$$$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$
