Question Number 79452 by Vishal Sharma last updated on 25/Jan/20
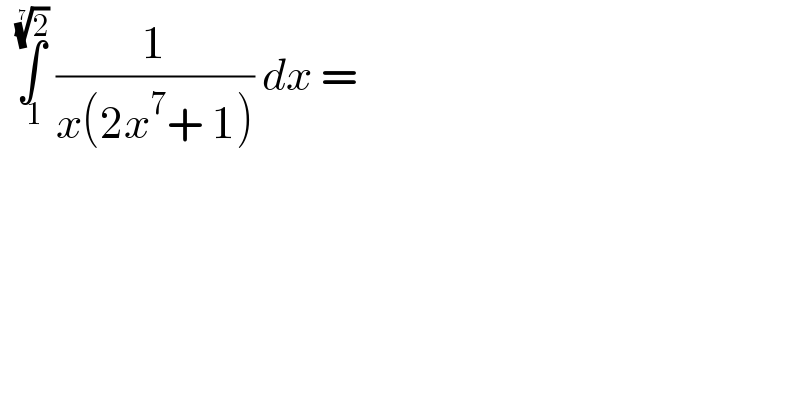
$$\:\:\underset{\:\mathrm{1}} {\overset{\sqrt[{\mathrm{7}}]{\mathrm{2}}} {\int}}\:\frac{\mathrm{1}}{{x}\left(\mathrm{2}{x}^{\mathrm{7}} +\:\mathrm{1}\right)}\:{dx}\:= \\ $$
Commented by john santu last updated on 25/Jan/20
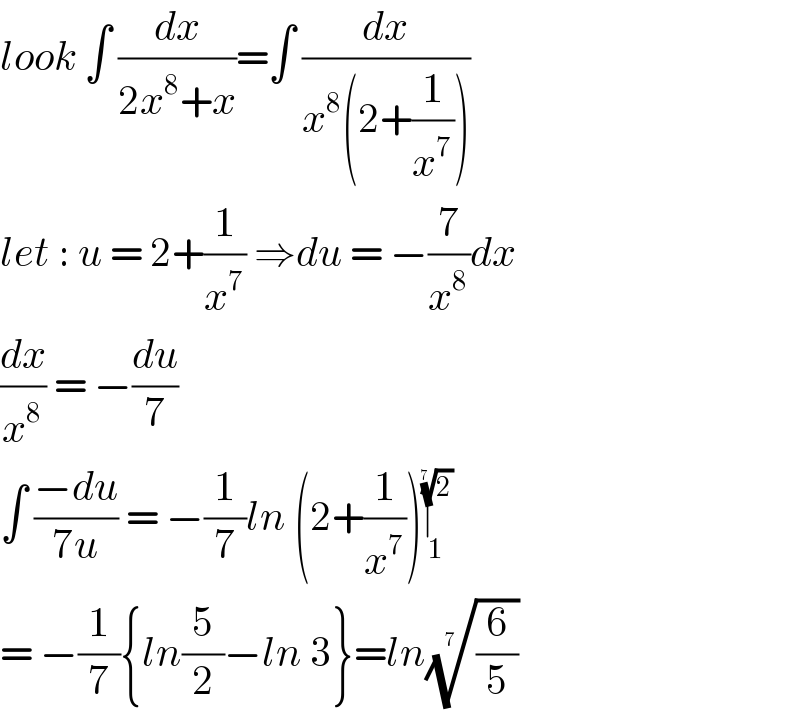
$${look}\:\int\:\frac{{dx}}{\mathrm{2}{x}^{\mathrm{8}} +{x}}=\int\:\frac{{dx}}{{x}^{\mathrm{8}} \left(\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{7}} }\right)} \\ $$$${let}\::\:{u}\:=\:\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{7}} }\:\Rightarrow{du}\:=\:−\frac{\mathrm{7}}{{x}^{\mathrm{8}} }{dx} \\ $$$$\frac{{dx}}{{x}^{\mathrm{8}} }\:=\:−\frac{{du}}{\mathrm{7}} \\ $$$$\int\:\frac{−{du}}{\mathrm{7}{u}}\:=\:−\frac{\mathrm{1}}{\mathrm{7}}{ln}\:\left(\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{7}} }\right)\underset{\mathrm{1}} {\overset{\sqrt[{\mathrm{7}\:}]{\mathrm{2}}} {\mid}} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{7}}\left\{{ln}\frac{\mathrm{5}}{\mathrm{2}}−{ln}\:\mathrm{3}\right\}={ln}\sqrt[{\mathrm{7}\:}]{\frac{\mathrm{6}}{\mathrm{5}}} \\ $$
Answered by mind is power last updated on 25/Jan/20

$$=\int\frac{{x}^{\mathrm{6}} }{{x}^{\mathrm{7}} \left(\mathrm{2}{x}^{\mathrm{7}} +\mathrm{1}\right)}{dx} \\ $$$${put}\:{y}={x}^{\mathrm{7}} \\ $$
