Question Number 21467 by nawroozdawry last updated on 24/Sep/17
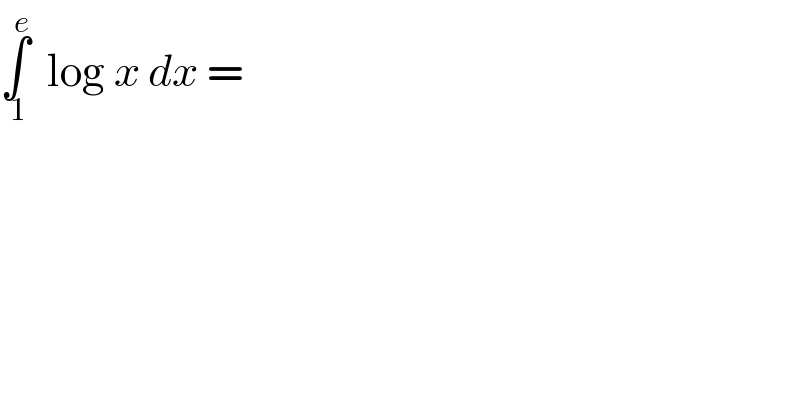
$$\underset{\:\mathrm{1}} {\overset{{e}} {\int}}\:\:\mathrm{log}\:{x}\:{dx}\:= \\ $$
Answered by $@ty@m last updated on 24/Sep/17
![I=∫logx.1dx =logx∫1dx−∫(1/x).xdx =xlogx−x+C ∴∫_1 ^e logxdx=[xlogx−x]_1 ^e =(eloge−e)−(log 1−1) =e−e−0+1 =1](https://www.tinkutara.com/question/Q21477.png)
$${I}=\int\mathrm{log}{x}.\mathrm{1}{dx}\: \\ $$$$=\mathrm{log}{x}\int\mathrm{1}{dx}−\int\frac{\mathrm{1}}{{x}}.{xdx} \\ $$$$={x}\mathrm{log}{x}−{x}+{C}\: \\ $$$$\therefore\underset{\mathrm{1}} {\overset{{e}} {\int}}\mathrm{log}{xdx}=\left[{x}\mathrm{log}{x}−{x}\underset{\mathrm{1}} {\overset{{e}} {\right]}}\:\: \\ $$$$=\left({e}\mathrm{log}{e}−{e}\right)−\left(\mathrm{log}\:\mathrm{1}−\mathrm{1}\right)\: \\ $$$$={e}−{e}−\mathrm{0}+\mathrm{1} \\ $$$$=\mathrm{1} \\ $$
