Question Number 11737 by Tadagbé last updated on 30/Mar/17
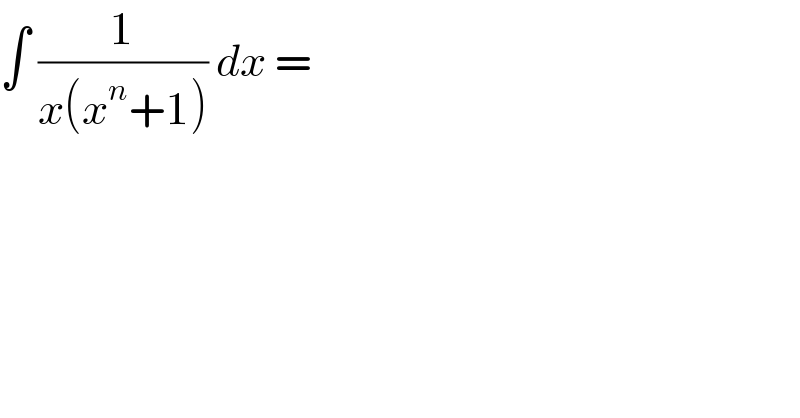
$$\int\:\frac{\mathrm{1}}{{x}\left({x}^{{n}} +\mathrm{1}\right)}\:{dx}\:= \\ $$
Answered by ajfour last updated on 30/Mar/17
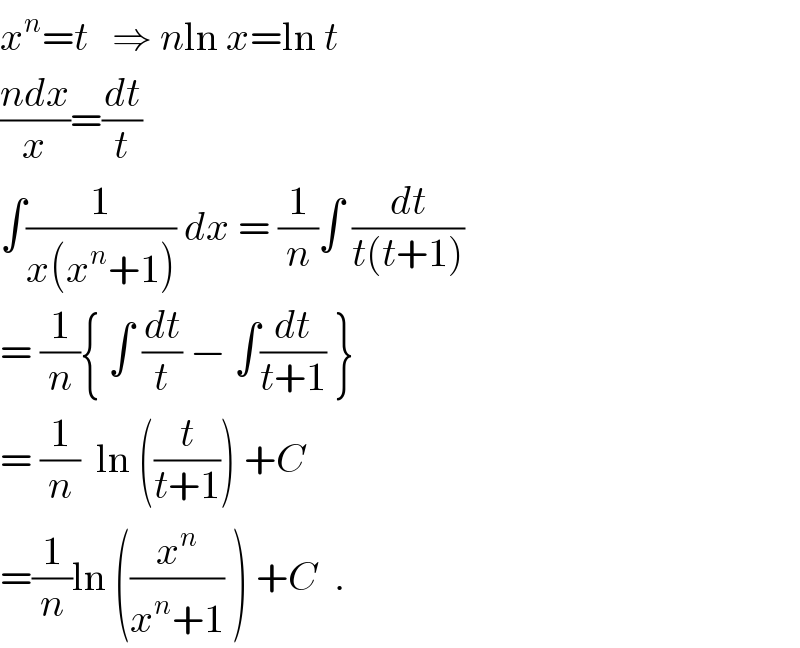
$${x}^{{n}} ={t}\:\:\:\Rightarrow\:{n}\mathrm{ln}\:{x}=\mathrm{ln}\:{t} \\ $$$$\frac{{ndx}}{{x}}=\frac{{dt}}{{t}} \\ $$$$\int\frac{\mathrm{1}}{{x}\left({x}^{{n}} +\mathrm{1}\right)}\:{dx}\:=\:\frac{\mathrm{1}}{{n}}\int\:\frac{{dt}}{{t}\left({t}+\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{1}}{{n}}\left\{\:\int\:\frac{{dt}}{{t}}\:−\:\int\frac{{dt}}{{t}+\mathrm{1}}\:\right\} \\ $$$$=\:\frac{\mathrm{1}}{{n}}\:\:\mathrm{ln}\:\left(\frac{{t}}{{t}+\mathrm{1}}\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{{n}}\mathrm{ln}\:\left(\frac{{x}^{{n}} }{{x}^{{n}} +\mathrm{1}}\:\right)\:+{C}\:\:. \\ $$
