Question Number 79435 by Vishal Sharma last updated on 25/Jan/20
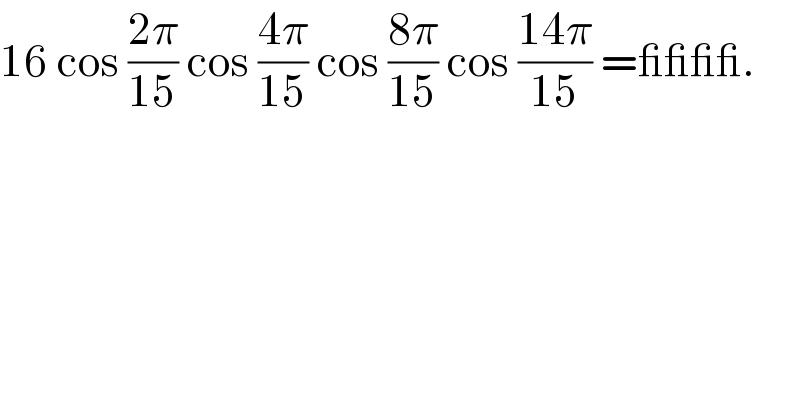
$$\mathrm{16}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{8}\pi}{\mathrm{15}}\:\mathrm{cos}\:\frac{\mathrm{14}\pi}{\mathrm{15}}\:=\_\_\_\_. \\ $$
Commented by jagoll last updated on 25/Jan/20
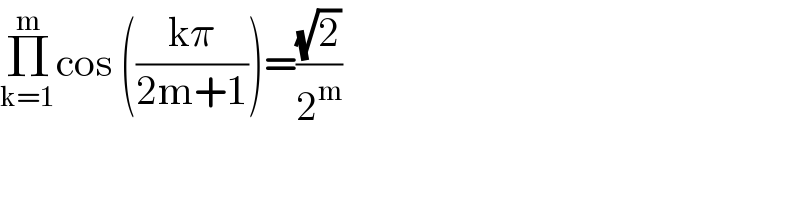
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{m}} {\prod}}\mathrm{cos}\:\left(\frac{\mathrm{k}\pi}{\mathrm{2m}+\mathrm{1}}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}^{\mathrm{m}} } \\ $$
