Question Number 55778 by gunawan last updated on 04/Mar/19
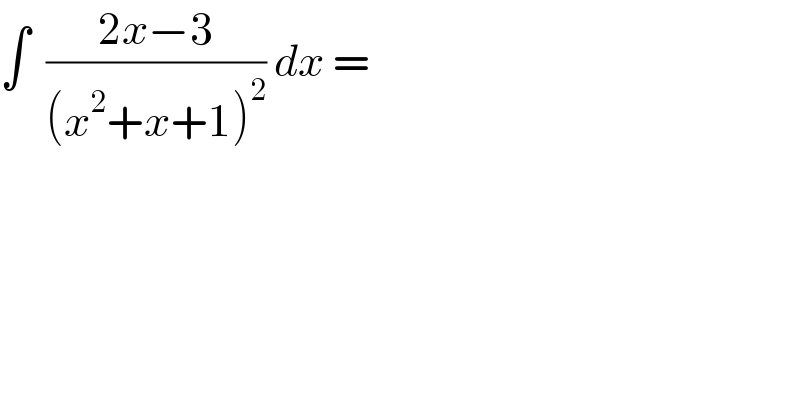
$$\int\:\:\frac{\mathrm{2}{x}−\mathrm{3}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:= \\ $$
Answered by MJS last updated on 04/Mar/19
![∫((2x−3)/((x^2 +x+1)^2 ))dx= =∫((2x+1)/((x^2 +x+1)^2 ))dx−4∫(dx/((x^2 +x+1)^2 )) (1) ∫((2x+1)/((x^2 +x+1)^2 ))dx= [t=x^2 +x+1 → dx=(dt/(2x+1))] =∫(dt/t^2 )=−(1/t)=−(1/(x^2 +x+1)) (2) −4∫(dx/((x^2 +x+1)^2 ))=−4∫(dx/(((x+(1/2))^2 +(3/4))^2 ))=−64∫(dx/(((2x+1)^2 +3)^2 ))= [t=2x+1 → dx=(dt/2)] =−32∫(dt/((t^2 +3)^2 ))= [reduction formula ∫(dt/((at^2 +b)^n ))=(t/(2b(n−1)(at^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(1/((at^2 +b)^(n−1) ))] =−((16t)/(3(t^2 +3)))−((16)/3)∫(dt/(t^2 +3))= =−((16t)/(3(t^2 +3)))−((16(√3))/9)arctan (((√3)t)/3)= =−((16(2x+1))/(3((2x+1)^2 +3)))−((16(√3))/9)arctan (((√3)(2x+1))/3) (1)+(2) −((8x+7)/(3(x^2 +x+1)))−((16(√3))/9)arctan (((√3)(2x+1))/3) +C](https://www.tinkutara.com/question/Q55801.png)
$$\int\frac{\mathrm{2}{x}−\mathrm{3}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\int\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}−\mathrm{4}\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left(\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{2}{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{2}} +{x}+\mathrm{1}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}+\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}} }=−\frac{\mathrm{1}}{{t}}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\left(\mathrm{2}\right) \\ $$$$−\mathrm{4}\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=−\mathrm{4}\int\frac{{dx}}{\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }=−\mathrm{64}\int\frac{{dx}}{\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{x}+\mathrm{1}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}}\right] \\ $$$$=−\mathrm{32}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{reduction}\:\mathrm{formula}\:\int\frac{{dt}}{\left({at}^{\mathrm{2}} +{b}\right)^{{n}} }=\frac{{t}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)\left({at}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }+\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)}\int\frac{\mathrm{1}}{\left({at}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }\right] \\ $$$$=−\frac{\mathrm{16}{t}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{16}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}= \\ $$$$=−\frac{\mathrm{16}{t}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}}= \\ $$$$=−\frac{\mathrm{16}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right) \\ $$$$−\frac{\mathrm{8}{x}+\mathrm{7}}{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}−\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:+{C} \\ $$
Commented by MJS last updated on 04/Mar/19
![−32∫(dt/((t^2 +3)^2 ))= [u=((√3)/3)t → dt=(√3)du] =−((32(√3))/9)∫(du/((u^2 +1)^2 ))= [v=2arctan u → du=(dv/(1+cos v))] =−((8(√3))/9)∫(1+cos v)dv= =−((8(√3))/9)(v+sin v)=−((16(√3)u)/(9(u^2 +1)))−((16(√3))/9)arctan u = =−((16t)/(3(t^2 +3)))−((16(√3))/9)arctan (((√3)t)/3)](https://www.tinkutara.com/question/Q55804.png)
$$−\mathrm{32}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{t}\:\rightarrow\:{dt}=\sqrt{\mathrm{3}}{du}\right] \\ $$$$=−\frac{\mathrm{32}\sqrt{\mathrm{3}}}{\mathrm{9}}\int\frac{{du}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[{v}=\mathrm{2arctan}\:{u}\:\rightarrow\:{du}=\frac{{dv}}{\mathrm{1}+\mathrm{cos}\:{v}}\right] \\ $$$$=−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\int\left(\mathrm{1}+\mathrm{cos}\:{v}\right){dv}= \\ $$$$=−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\left({v}+\mathrm{sin}\:{v}\right)=−\frac{\mathrm{16}\sqrt{\mathrm{3}}{u}}{\mathrm{9}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:{u}\:= \\ $$$$=−\frac{\mathrm{16}{t}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{t}}{\mathrm{3}} \\ $$
