Question Number 54029 by qw last updated on 28/Jan/19
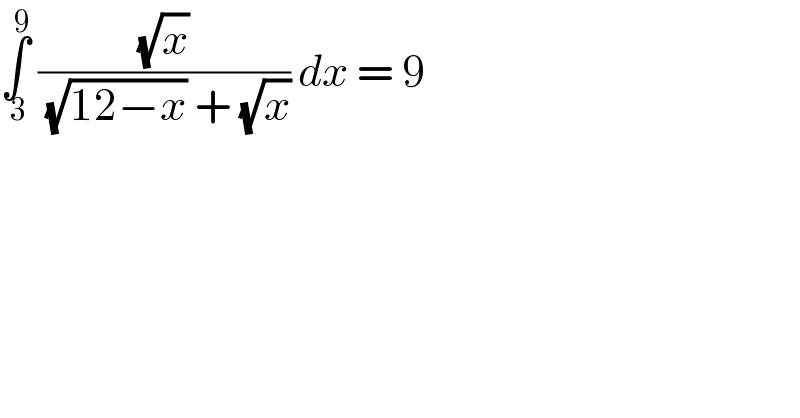
$$\underset{\:\mathrm{3}} {\overset{\mathrm{9}} {\int}}\:\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{12}−{x}}\:+\:\sqrt{{x}}}\:{dx}\:=\:\mathrm{9} \\ $$
Commented by maxmathsup by imad last updated on 29/Jan/19
![let prove that ∫_a ^b f(x)dx =∫_a ^b f(a+b−x)dx for all function intehrable on]a,b[ chang.a+b −x =t give ∫_a ^b f(a+b−x)dx =∫_b ^a f(t)(−dt) =∫_a ^b f(t)dt the result is proved let A =∫_3 ^9 ((√x)/( (√(12−x))+(√x))) dx the result give A =∫_3 ^9 ((√(12−x))/( (√x)+(√(12−x)))) dx ⇒2A =A +A =∫_3 ^9 {((√x)/( (√(12−x))+(√x))) +((√(12−x))/( (√x)+(√(12−x))))}dx =∫_3 ^9 dx =6 ⇒2A =6 ⇒A =3 .](https://www.tinkutara.com/question/Q54149.png)
$$\left.{let}\:{prove}\:{that}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:=\int_{{a}} ^{{b}} \:{f}\left({a}+{b}−{x}\right){dx}\:{for}\:{all}\:{function}\:{intehrable}\:{on}\right]{a},{b}\left[\right. \\ $$$${chang}.{a}+{b}\:−{x}\:={t}\:{give}\:\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx}\:=\int_{{b}} ^{{a}} {f}\left({t}\right)\left(−{dt}\right)\:=\int_{{a}} ^{{b}} {f}\left({t}\right){dt} \\ $$$${the}\:{result}\:{is}\:{proved}\:{let}\:{A}\:=\int_{\mathrm{3}} ^{\mathrm{9}} \:\:\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{12}−{x}}+\sqrt{{x}}}\:{dx}\:\:{the}\:{result}\:{give} \\ $$$${A}\:=\int_{\mathrm{3}} ^{\mathrm{9}} \:\:\frac{\sqrt{\mathrm{12}−{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{12}−{x}}}\:{dx}\:\Rightarrow\mathrm{2}{A}\:={A}\:+{A}\:=\int_{\mathrm{3}} ^{\mathrm{9}} \left\{\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{12}−{x}}+\sqrt{{x}}}\:+\frac{\sqrt{\mathrm{12}−{x}}}{\:\sqrt{{x}}+\sqrt{\mathrm{12}−{x}}}\right\}{dx} \\ $$$$\:=\int_{\mathrm{3}} ^{\mathrm{9}} \:{dx}\:=\mathrm{6}\:\Rightarrow\mathrm{2}{A}\:=\mathrm{6}\:\Rightarrow{A}\:=\mathrm{3}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jan/19
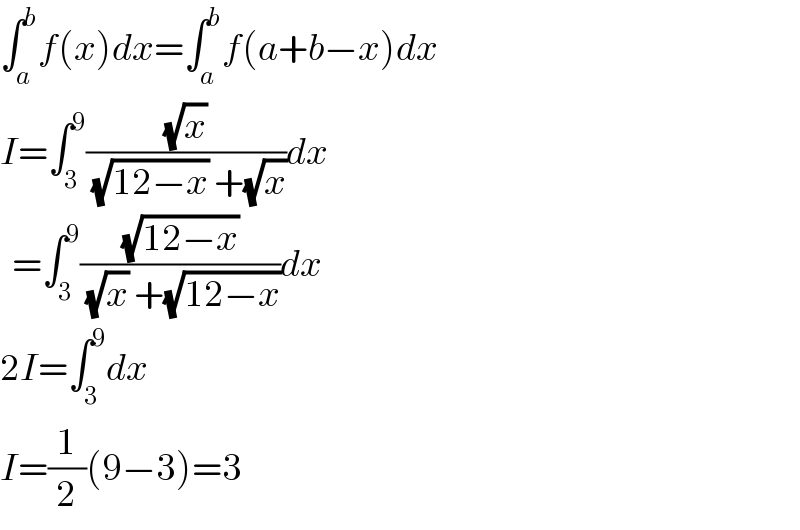
$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$${I}=\int_{\mathrm{3}} ^{\mathrm{9}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{12}−{x}}\:+\sqrt{{x}}}{dx} \\ $$$$\:\:=\int_{\mathrm{3}} ^{\mathrm{9}} \frac{\sqrt{\mathrm{12}−{x}}}{\:\sqrt{{x}}\:+\sqrt{\mathrm{12}−{x}}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{3}} ^{\mathrm{9}} {dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}−\mathrm{3}\right)=\mathrm{3} \\ $$
