Menu Close

5-men-or-10-women-can-complete-a-work-in-20-days-In-how-many-days-can-3-men-and-4-women-complete-it-

Tinku Tara 0 Comments
Pin




Question Number 7467 by Obenfo last updated on 30/Aug/16
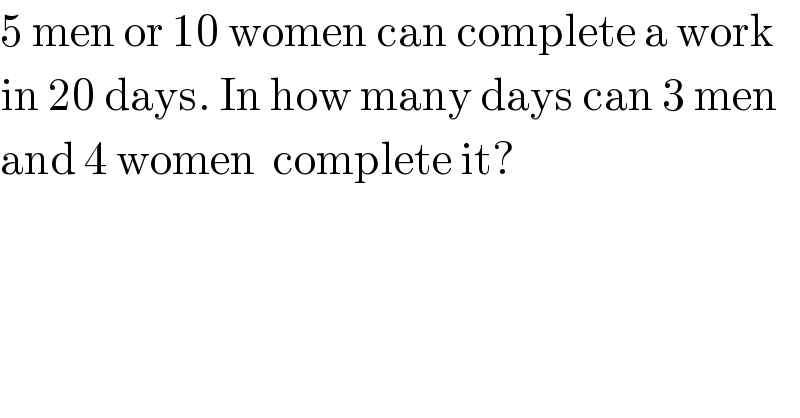
5 men or 10 women can complete a work in 20 days. In how many days can 3 men and 4 women complete it?
$$\mathrm{5}\:\mathrm{men}\:\mathrm{or}\:\mathrm{10}\:\mathrm{women}\:\mathrm{can}\:\mathrm{complete}\:\mathrm{a}\:\mathrm{work} \\ $$$$\mathrm{in}\:\mathrm{20}\:\mathrm{days}.\:\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{days}\:\mathrm{can}\:\mathrm{3}\:\mathrm{men} \\ $$$$\mathrm{and}\:\mathrm{4}\:\mathrm{women}\:\:\mathrm{complete}\:\mathrm{it}? \\ $$
Commented by FilupSmith last updated on 31/Aug/16
attempt − unsure if correct. 5m=20 ⇒ m=4 10w=20 ⇒ w=2 x=3m+4w=3(4)+4(2) x=12+8 x=20
$$\mathrm{attempt}\:−\:\mathrm{unsure}\:\mathrm{if}\:\mathrm{correct}. \\ $$$$ \\ $$$$\mathrm{5}{m}=\mathrm{20}\:\Rightarrow\:{m}=\mathrm{4} \\ $$$$\mathrm{10}{w}=\mathrm{20}\:\Rightarrow\:{w}=\mathrm{2} \\ $$$$ \\ $$$${x}=\mathrm{3}{m}+\mathrm{4}{w}=\mathrm{3}\left(\mathrm{4}\right)+\mathrm{4}\left(\mathrm{2}\right) \\ $$$${x}=\mathrm{12}+\mathrm{8} \\ $$$${x}=\mathrm{20} \\ $$
Answered by Rasheed Soomro last updated on 31/Aug/16
5 men=10 woman 1 man=2 women 3 men=6 women 3 men+4 women=6 women+4 women=10 women 10 women can complete a work in 20 days [Given] ∴3 men+4 women can complete a work in 20 days
$$\mathrm{5}\:{men}=\mathrm{10}\:{woman} \\ $$$$\mathrm{1}\:{man}=\mathrm{2}\:{women} \\ $$$$\mathrm{3}\:{men}=\mathrm{6}\:{women} \\ $$$$\mathrm{3}\:{men}+\mathrm{4}\:{women}=\mathrm{6}\:{women}+\mathrm{4}\:{women}=\mathrm{10}\:{women} \\ $$$$\mathrm{10}\:{women}\:{can}\:{complete}\:{a}\:{work}\:{in}\:\mathrm{20}\:{days}\:\left[{Given}\right] \\ $$$$\therefore\mathrm{3}\:{men}+\mathrm{4}\:{women}\:{can}\:{complete}\:{a}\:{work}\:{in}\:\mathrm{20}\:{days} \\ $$$$ \\ $$
Commented by sandy_suhendra last updated on 31/Aug/16
Great approach!
$${Great}\:{approach}! \\ $$
Answered by sandy_suhendra last updated on 31/Aug/16
another answer 5 men = 20 days ⇒ 1 man = 100 days 1 man in 1 day = (1/(100)) part of work 3 men in 1 day = (3/(100)) part of work 10 women = 20 days ⇒ 1 woman = 200 days 1 woman in 1 day = (1/(200)) part of work 4 women in 1 day = (4/(200)) = (1/(50)) part of work 3 men and 4 women in 1 day = (3/(100))+(1/(50))=(1/(20)) part of work so 3 men and 4 women can complete the work in 20 days
$${another}\:{answer} \\ $$$$\mathrm{5}\:{men}\:=\:\mathrm{20}\:{days}\:\Rightarrow\:\mathrm{1}\:{man}\:=\:\mathrm{100}\:{days} \\ $$$$\mathrm{1}\:{man}\:{in}\:\mathrm{1}\:{day}\:=\:\frac{\mathrm{1}}{\mathrm{100}}\:{part}\:{of}\:{work} \\ $$$$\mathrm{3}\:{men}\:{in}\:\mathrm{1}\:{day}\:=\:\frac{\mathrm{3}}{\mathrm{100}}\:{part}\:{of}\:{work} \\ $$$$\mathrm{10}\:{women}\:=\:\mathrm{20}\:{days}\:\Rightarrow\:\mathrm{1}\:{woman}\:=\:\mathrm{200}\:{days} \\ $$$$\mathrm{1}\:{woman}\:{in}\:\mathrm{1}\:{day}\:=\:\frac{\mathrm{1}}{\mathrm{200}}\:{part}\:{of}\:{work} \\ $$$$\mathrm{4}\:{women}\:{in}\:\mathrm{1}\:{day}\:=\:\frac{\mathrm{4}}{\mathrm{200}}\:=\:\frac{\mathrm{1}}{\mathrm{50}}\:{part}\:{of}\:{work} \\ $$$$\mathrm{3}\:{men}\:{and}\:\mathrm{4}\:{women}\:{in}\:\mathrm{1}\:{day}\:=\:\frac{\mathrm{3}}{\mathrm{100}}+\frac{\mathrm{1}}{\mathrm{50}}=\frac{\mathrm{1}}{\mathrm{20}}\:{part}\:{of}\:{work} \\ $$$${so}\:\mathrm{3}\:{men}\:{and}\:\mathrm{4}\:{women}\:{can}\:{complete}\:{the}\:{work}\:{in}\:\mathrm{20}\:{days} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *