666-6-2-n-digits-888-8-n-digits-is-equal-to-

Question Number 56416 by gunawan last updated on 16/Mar/19

\underset{n - digits}{{(666 \dots . 6)}^{2}} + \underset{n - digits}{(888 \dots . 8)} is equal to

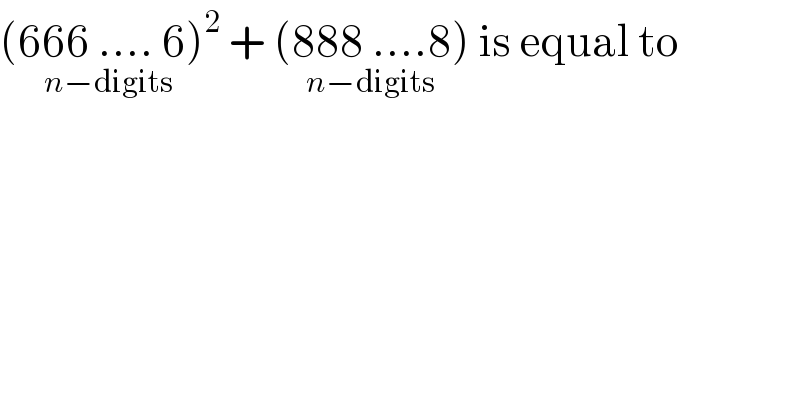
Commented by mr W last updated on 16/Mar/19

= \underset{2 n d i g i t s}{(444 \dots 4)}

Answered by tanmay.chaudhury50@gmail.com last updated on 16/Mar/19

(666 \dots . 6) \leftarrow n d i g i t

6 (111 \dots 1)

6 {10^{n - 1} + 10^{n - 2} + 10^{n - 3} + \dots + 1}

6 \times \frac{10^{n - 1} (1 - \frac{1}{10^{n}})}{(1 - \frac{1}{10})} \to \frac{6}{9} \times 10^{n} (\frac{10^{n} - 1}{10^{n}}) \to \frac{6}{9} (10^{n} - 1)

s o a n s w e r i s

\frac{36}{81} {(10^{n} - 1)}^{2} + \frac{8}{9} (10^{n} - 1)

{\frac{4}{9} {(10^{n} - 1)}^{2}} + \frac{8}{9} (10^{n} - 1)

\frac{4}{9} (10^{n} - 1) (10^{n} - 1 + 2)

\frac{4}{9} (10^{2 n} - 1)

4 (\frac{10^{2 n} - 1}{10 - 1})

[a (\frac{r^{n} - 1}{r - 1}) = a + a r + {a r}^{2} + \dots + {a r}^{n}]

4 (1 + 10 + 10^{2} + 10^{3} + \dots + 10^{2 n})

(4 + 40 + 400 + 4000 + \dots . .)

(444 \dots . 4) \leftarrow 2 n d i g i t

Commented by mr W last updated on 16/Mar/19

g o o d j o b s i r!

Commented by tanmay.chaudhury50@gmail.com last updated on 16/Mar/19

t h s n k y o u s i r \dots