Question Number 24998 by anuj saini last updated on 30/Nov/17

$$\mathrm{A}\:\mathrm{fair}\:\mathrm{coin}\:\mathrm{is}\:\mathrm{tossed}\:\mathrm{100}\:\mathrm{times}.\:\mathrm{The} \\ $$$$\mathrm{probability}\:\mathrm{of}\:\mathrm{getting}\:\mathrm{tails}\:\mathrm{an}\:\mathrm{odd} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{times}\:\mathrm{is} \\ $$
Commented by Penguin last updated on 01/Dec/17
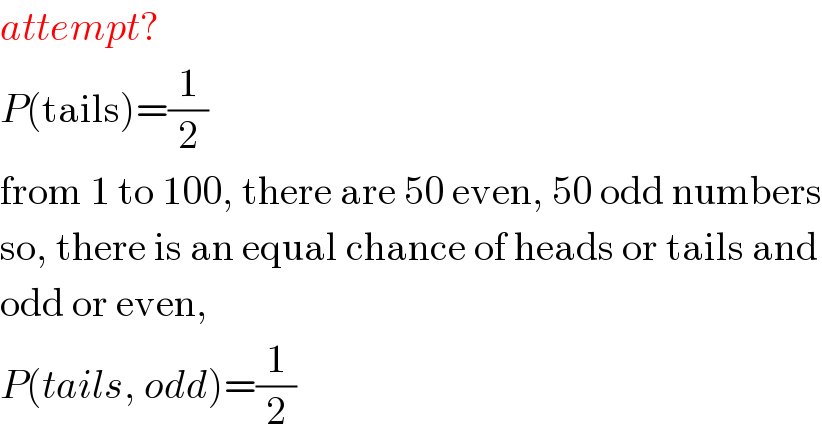
$${attempt}? \\ $$$${P}\left(\mathrm{tails}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{100},\:\mathrm{there}\:\mathrm{are}\:\mathrm{50}\:\mathrm{even},\:\mathrm{50}\:\mathrm{odd}\:\mathrm{numbers} \\ $$$$\mathrm{so},\:\mathrm{there}\:\mathrm{is}\:\mathrm{an}\:\mathrm{equal}\:\mathrm{chance}\:\mathrm{of}\:\mathrm{heads}\:\mathrm{or}\:\mathrm{tails}\:\mathrm{and} \\ $$$$\mathrm{odd}\:\mathrm{or}\:\mathrm{even}, \\ $$$${P}\left({tails},\:{odd}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 01/Dec/17

$$\mathrm{Question}\:\mathrm{is}\:\mathrm{asking}\:\mathrm{for}\:\mathrm{a}\:\mathrm{probablity} \\ $$$$\mathrm{that}\:\mathrm{odd}\:\mathrm{number}\:\mathrm{of}\:\mathrm{tails} \\ $$$$\mathrm{you}\:\mathrm{are}\:\mathrm{correct}\:\mathrm{in}\:\mathrm{saying}\:\mathrm{that} \\ $$$$\mathrm{probablity}\:\mathrm{of}\:\mathrm{odd}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{tails}=\mathrm{odd}\:\mathrm{number}\:\mathrm{of}\:\mathrm{heads}. \\ $$$$\mathrm{However}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{above}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{1}\:\mathrm{since}\:\mathrm{that}\:\mathrm{are}\:\mathrm{cases}\:\mathrm{that} \\ $$$$\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{even}\:\mathrm{number}\:\mathrm{of}\:\mathrm{heads} \\ $$$$\mathrm{and}\:\mathrm{tails}. \\ $$
