Menu Close

A-father-with-8-children-takes-3-at-a-time-to-the-garden-as-often-as-he-without-taking-the-same-3-children-together-more-than-once-The-number-of-times-he-will-go-to-the-garden-is-

Tinku Tara 0 Comments
Pin




Question Number 63490 by kumaranjul306@gmail.com last updated on 04/Jul/19
A father with 8 children takes 3 at a time to the garden as often as he without taking the same 3 children together more than once. The number of times he will go to the garden is
$$\mathrm{A}\:\mathrm{father}\:\mathrm{with}\:\mathrm{8}\:\mathrm{children}\:\mathrm{takes}\:\mathrm{3}\:\mathrm{at}\:\mathrm{a}\: \\ $$$$\mathrm{time}\:\mathrm{to}\:\mathrm{the}\:\mathrm{garden}\:\mathrm{as}\:\mathrm{often}\:\mathrm{as}\:\mathrm{he} \\ $$$$\mathrm{without}\:\mathrm{taking}\:\mathrm{the}\:\mathrm{same}\:\mathrm{3}\:\mathrm{children} \\ $$$$\mathrm{together}\:\mathrm{more}\:\mathrm{than}\:\mathrm{once}.\:\mathrm{The}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{times}\:\mathrm{he}\:\mathrm{will}\:\mathrm{go}\:\mathrm{to}\:\mathrm{the}\:\mathrm{garden}\:\mathrm{is} \\ $$
Commented by Prithwish sen last updated on 05/Jul/19
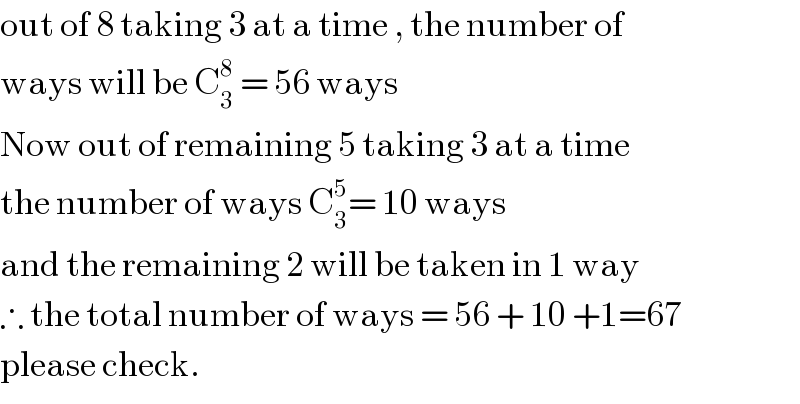
out of 8 taking 3 at a time , the number of ways will be C_3 ^8 = 56 ways Now out of remaining 5 taking 3 at a time the number of ways C_3 ^5 = 10 ways and the remaining 2 will be taken in 1 way ∴ the total number of ways = 56 + 10 +1=67 please check.
$$\mathrm{out}\:\mathrm{of}\:\mathrm{8}\:\mathrm{taking}\:\mathrm{3}\:\mathrm{at}\:\mathrm{a}\:\mathrm{time}\:,\:\mathrm{the}\:\mathrm{number}\:\mathrm{of} \\ $$$$\mathrm{ways}\:\mathrm{will}\:\mathrm{be}\:\mathrm{C}_{\mathrm{3}} ^{\mathrm{8}} \:=\:\mathrm{56}\:\mathrm{ways} \\ $$$$\mathrm{Now}\:\mathrm{out}\:\mathrm{of}\:\mathrm{remaining}\:\mathrm{5}\:\mathrm{taking}\:\mathrm{3}\:\mathrm{at}\:\mathrm{a}\:\mathrm{time} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{C}_{\mathrm{3}} ^{\mathrm{5}} =\:\mathrm{10}\:\mathrm{ways} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{2}\:\mathrm{will}\:\mathrm{be}\:\mathrm{taken}\:\mathrm{in}\:\mathrm{1}\:\mathrm{way} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:=\:\mathrm{56}\:+\:\mathrm{10}\:+\mathrm{1}=\mathrm{67} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Answered by Rio Michael last updated on 05/Jul/19
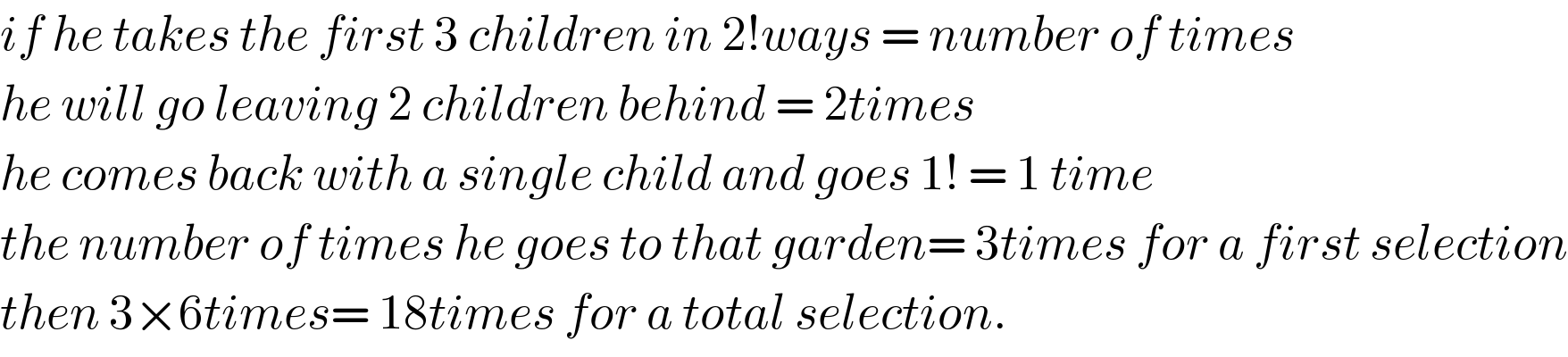
if he takes the first 3 children in 2!ways = number of times he will go leaving 2 children behind = 2times he comes back with a single child and goes 1! = 1 time the number of times he goes to that garden= 3times for a first selection then 3×6times= 18times for a total selection.
$${if}\:{he}\:{takes}\:{the}\:{first}\:\mathrm{3}\:{children}\:{in}\:\mathrm{2}!{ways}\:=\:{number}\:{of}\:{times} \\ $$$${he}\:{will}\:{go}\:{leaving}\:\mathrm{2}\:{children}\:{behind}\:=\:\mathrm{2}{times} \\ $$$${he}\:{comes}\:{back}\:{with}\:{a}\:{single}\:{child}\:{and}\:{goes}\:\mathrm{1}!\:=\:\mathrm{1}\:{time} \\ $$$${the}\:{number}\:{of}\:{times}\:{he}\:{goes}\:{to}\:{that}\:{garden}=\:\mathrm{3}{times}\:{for}\:{a}\:{first}\:{selection} \\ $$$${then}\:\mathrm{3}×\mathrm{6}{times}=\:\mathrm{18}{times}\:{for}\:{a}\:{total}\:{selection}. \\ $$
Answered by ajfour last updated on 05/Jul/19
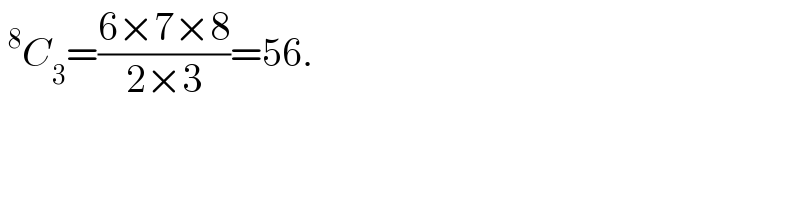
^8 C_3 =((6×7×8)/(2×3))=56.
$$\:^{\mathrm{8}} {C}_{\mathrm{3}} =\frac{\mathrm{6}×\mathrm{7}×\mathrm{8}}{\mathrm{2}×\mathrm{3}}=\mathrm{56}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *