Question Number 25076 by Mr easy last updated on 03/Dec/17
![A man can row 6 km/h in still water. When the river is running at 1.2 km/h, it takes]him 1 hour to row to a place and back. How far is the place?](https://www.tinkutara.com/question/Q25076.png)
$$\mathrm{A}\:\mathrm{man}\:\mathrm{can}\:\mathrm{row}\:\mathrm{6}\:\mathrm{km}/\mathrm{h}\:\mathrm{in}\:\mathrm{still}\:\mathrm{water}. \\ $$$$\mathrm{When}\:\mathrm{the}\:\mathrm{river}\:\mathrm{is}\:\mathrm{running}\:\mathrm{at}\:\mathrm{1}.\mathrm{2}\:\mathrm{km}/\mathrm{h}, \\ $$$$\left.\mathrm{it}\:\mathrm{takes}\right]\mathrm{him}\:\mathrm{1}\:\mathrm{hour}\:\mathrm{to}\:\mathrm{row}\:\mathrm{to}\:\mathrm{a}\:\mathrm{place}\: \\ $$$$\mathrm{and}\:\mathrm{back}.\:\mathrm{How}\:\mathrm{far}\:\mathrm{is}\:\mathrm{the}\:\mathrm{place}? \\ $$
Answered by mrW1 last updated on 03/Dec/17
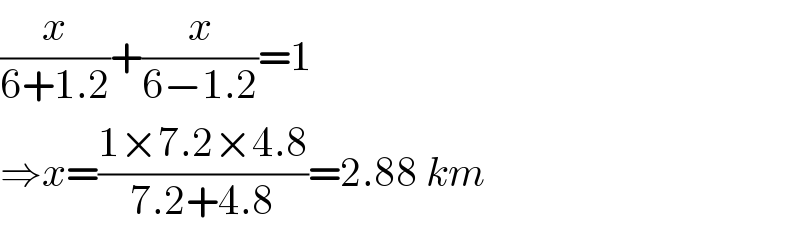
$$\frac{{x}}{\mathrm{6}+\mathrm{1}.\mathrm{2}}+\frac{{x}}{\mathrm{6}−\mathrm{1}.\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}×\mathrm{7}.\mathrm{2}×\mathrm{4}.\mathrm{8}}{\mathrm{7}.\mathrm{2}+\mathrm{4}.\mathrm{8}}=\mathrm{2}.\mathrm{88}\:{km} \\ $$
