Question Number 7487 by Obenfo last updated on 31/Aug/16

$$\mathrm{A}\:\mathrm{person}\:\mathrm{can}\:\mathrm{swim}\:\mathrm{at}\:\mathrm{the}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{5}\:\mathrm{kmph} \\ $$$$\mathrm{upstream}\:\mathrm{and}\:\mathrm{13}\:\mathrm{kmph}\:\mathrm{downstream}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{time}\:\mathrm{taken}\:\mathrm{by}\:\mathrm{the}\:\mathrm{person}\:\mathrm{to}\: \\ $$$$\mathrm{swim}\:\mathrm{10}\:\mathrm{metres}\:\mathrm{in}\:\mathrm{still}\:\mathrm{water}. \\ $$
Answered by prakash jain last updated on 31/Aug/16
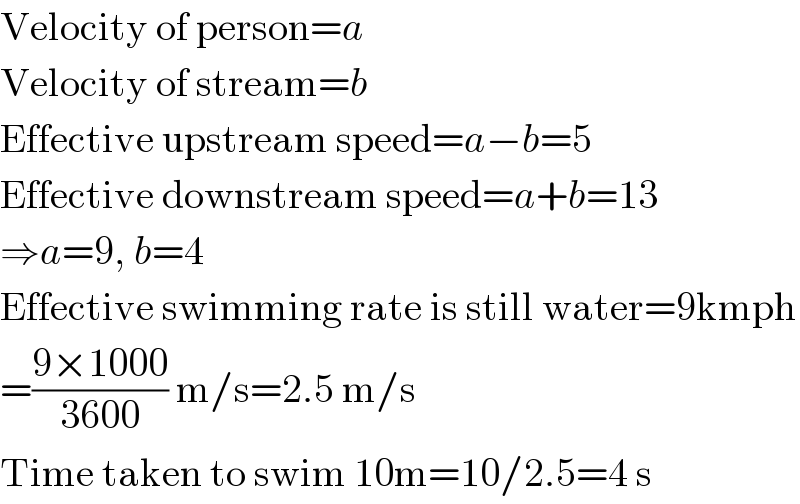
$$\mathrm{Velocity}\:\mathrm{of}\:\mathrm{person}={a} \\ $$$$\mathrm{Velocity}\:\mathrm{of}\:\mathrm{stream}={b} \\ $$$$\mathrm{Effective}\:\mathrm{upstream}\:\mathrm{speed}={a}−{b}=\mathrm{5} \\ $$$$\mathrm{Effective}\:\mathrm{downstream}\:\mathrm{speed}={a}+{b}=\mathrm{13} \\ $$$$\Rightarrow{a}=\mathrm{9},\:{b}=\mathrm{4} \\ $$$$\mathrm{Effective}\:\mathrm{swimming}\:\mathrm{rate}\:\mathrm{is}\:\mathrm{still}\:\mathrm{water}=\mathrm{9kmph} \\ $$$$=\frac{\mathrm{9}×\mathrm{1000}}{\mathrm{3600}}\:\mathrm{m}/\mathrm{s}=\mathrm{2}.\mathrm{5}\:\mathrm{m}/\mathrm{s} \\ $$$$\mathrm{Time}\:\mathrm{taken}\:\mathrm{to}\:\mathrm{swim}\:\mathrm{10m}=\mathrm{10}/\mathrm{2}.\mathrm{5}=\mathrm{4}\:\mathrm{s} \\ $$
