Question Number 53382 by gunawan last updated on 21/Jan/19
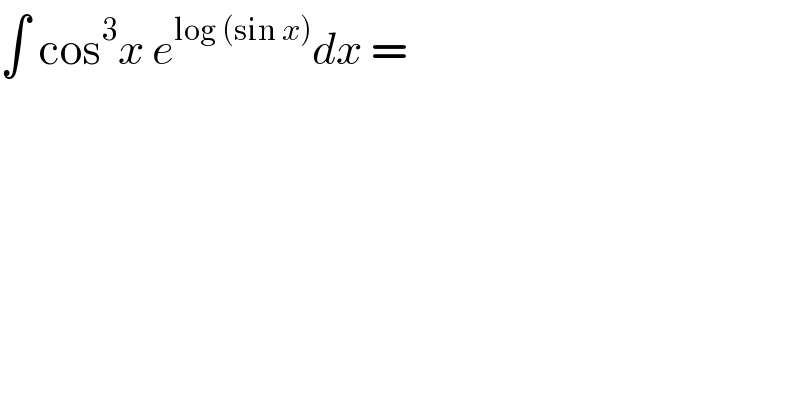
$$\int\:\mathrm{cos}^{\mathrm{3}} {x}\:{e}^{\mathrm{log}\:\left(\mathrm{sin}\:{x}\right)} {dx}\:= \\ $$
Answered by math1967 last updated on 21/Jan/19
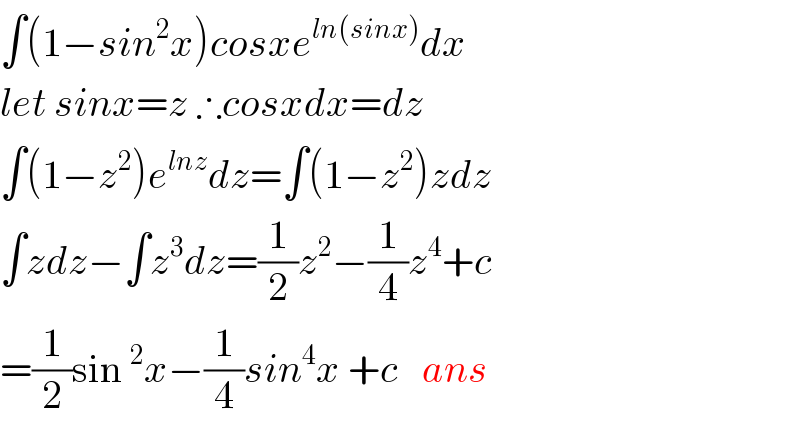
$$\int\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){cosxe}^{{ln}\left({sinx}\right)} {dx} \\ $$$${let}\:{sinx}={z}\:\therefore{cosxdx}={dz} \\ $$$$\int\left(\mathrm{1}−{z}^{\mathrm{2}} \right){e}^{{lnz}} {dz}=\int\left(\mathrm{1}−{z}^{\mathrm{2}} \right){zdz}\: \\ $$$$\int{zdz}−\int{z}^{\mathrm{3}} {dz}=\frac{\mathrm{1}}{\mathrm{2}}{z}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}{z}^{\mathrm{4}} +{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{4}}{sin}^{\mathrm{4}} {x}\:+{c}\:\:\:{ans} \\ $$
