Menu Close

cos-x-cos-3-x-1-cos-3-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 37188 by rahul 19 last updated on 10/Jun/18
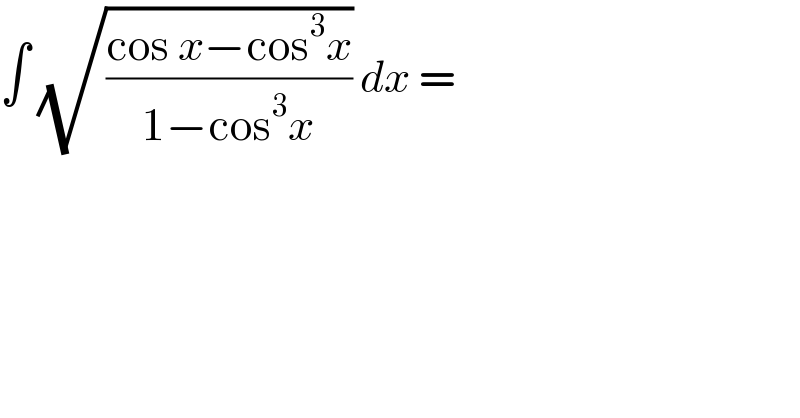
∫ (√((cos x−cos^3 x)/(1−cos^3 x))) dx =
$$\int\:\sqrt{\frac{\mathrm{cos}\:{x}−\mathrm{cos}^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{cos}^{\mathrm{3}} {x}}}\:{dx}\:= \\ $$
Answered by ajfour last updated on 10/Jun/18
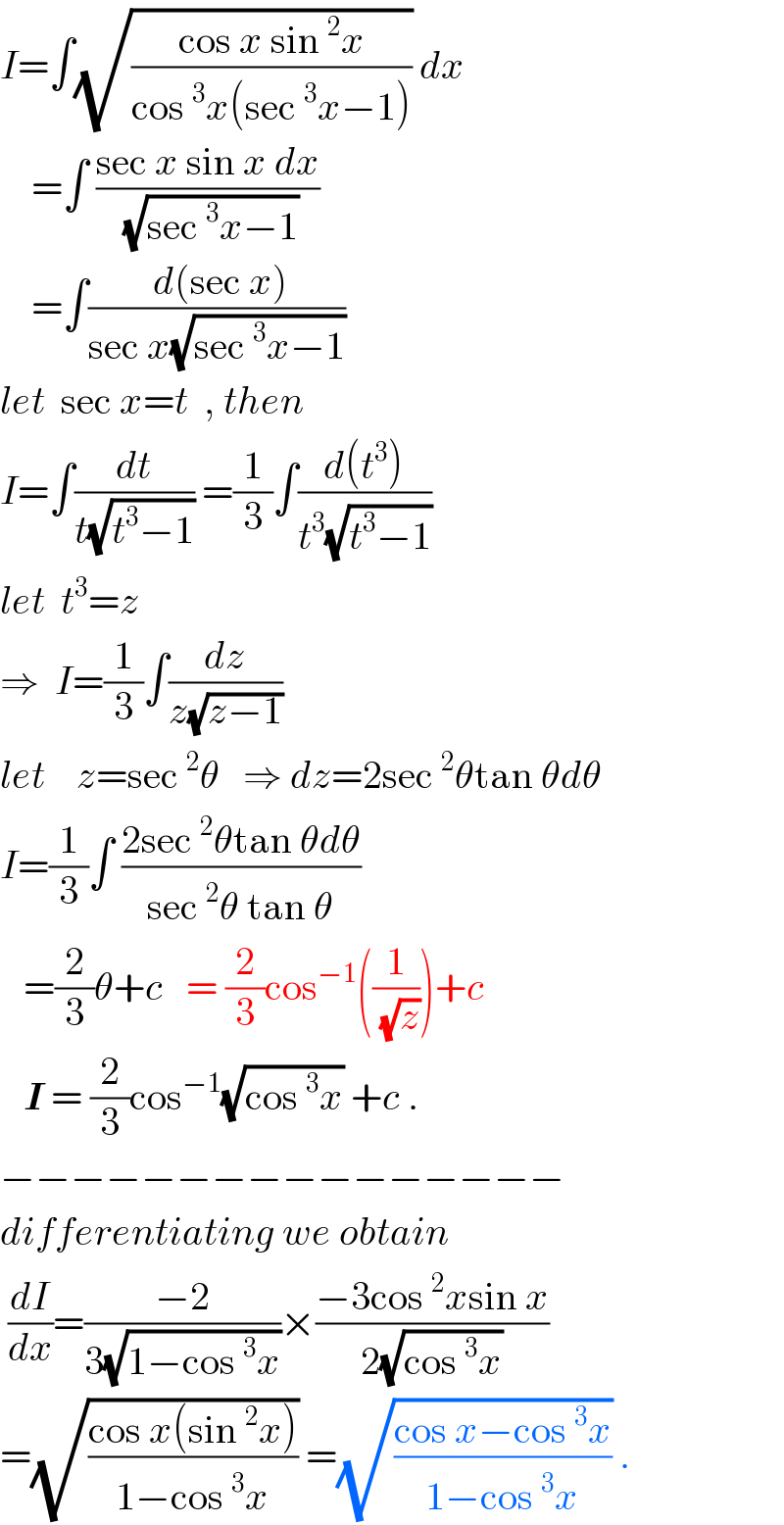
I=∫(√((cos x sin^2 x)/(cos^3 x(sec^3 x−1)))) dx =∫ ((sec x sin x dx)/( (√(sec^3 x−1)))) =∫(( d(sec x))/(sec x(√(sec^3 x−1)))) let sec x=t , then I=∫(dt/(t(√(t^3 −1)))) =(1/3)∫((d(t^3 ))/(t^3 (√(t^3 −1)))) let t^3 =z ⇒ I=(1/3)∫(dz/(z(√(z−1)))) let z=sec^2 θ ⇒ dz=2sec^2 θtan θdθ I=(1/3)∫ ((2sec^2 θtan θdθ)/(sec^2 θ tan θ)) =(2/3)θ+c = (2/3)cos^(−1) ((1/( (√z))))+c I = (2/3)cos^(−1) (√(cos^3 x)) +c . −−−−−−−−−−−−−−−− differentiating we obtain (dI/dx)=((−2)/(3(√(1−cos^3 x))))×((−3cos^2 xsin x)/(2(√(cos^3 x)))) =(√((cos x(sin^2 x))/(1−cos^3 x))) =(√((cos x−cos^3 x)/(1−cos^3 x))) .
$${I}=\int\sqrt{\frac{\mathrm{cos}\:{x}\:\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{3}} {x}\left(\mathrm{sec}\:^{\mathrm{3}} {x}−\mathrm{1}\right)}}\:{dx} \\ $$$$\:\:\:\:=\int\:\frac{\mathrm{sec}\:{x}\:\mathrm{sin}\:{x}\:{dx}}{\:\sqrt{\mathrm{sec}\:^{\mathrm{3}} {x}−\mathrm{1}}} \\ $$$$\:\:\:\:=\int\frac{\:{d}\left(\mathrm{sec}\:{x}\right)}{\mathrm{sec}\:{x}\sqrt{\mathrm{sec}\:^{\mathrm{3}} {x}−\mathrm{1}}} \\ $$$${let}\:\:\mathrm{sec}\:{x}={t}\:\:,\:{then} \\ $$$${I}=\int\frac{{dt}}{{t}\sqrt{{t}^{\mathrm{3}} −\mathrm{1}}}\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{d}\left({t}^{\mathrm{3}} \right)}{{t}^{\mathrm{3}} \sqrt{{t}^{\mathrm{3}} −\mathrm{1}}} \\ $$$${let}\:\:{t}^{\mathrm{3}} ={z} \\ $$$$\Rightarrow\:\:{I}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dz}}{{z}\sqrt{{z}−\mathrm{1}}} \\ $$$${let}\:\:\:\:{z}=\mathrm{sec}\:^{\mathrm{2}} \theta\:\:\:\Rightarrow\:{dz}=\mathrm{2sec}\:^{\mathrm{2}} \theta\mathrm{tan}\:\theta{d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{2sec}\:^{\mathrm{2}} \theta\mathrm{tan}\:\theta{d}\theta}{\mathrm{sec}\:^{\mathrm{2}} \theta\:\mathrm{tan}\:\theta} \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}\theta+{c}\:\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{{z}}}\right)+{c} \\ $$$$\:\:\:\boldsymbol{{I}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}^{−\mathrm{1}} \sqrt{\mathrm{cos}\:^{\mathrm{3}} {x}}\:+{c}\:. \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${differentiating}\:{we}\:{obtain} \\ $$$$\:\frac{{dI}}{{dx}}=\frac{−\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{3}} {x}}}×\frac{−\mathrm{3cos}\:^{\mathrm{2}} {x}\mathrm{sin}\:{x}}{\mathrm{2}\sqrt{\mathrm{cos}\:^{\mathrm{3}} {x}}} \\ $$$$=\sqrt{\frac{\mathrm{cos}\:{x}\left(\mathrm{sin}\:^{\mathrm{2}} {x}\right)}{\mathrm{1}−\mathrm{cos}\:^{\mathrm{3}} {x}}}\:=\sqrt{\frac{\mathrm{cos}\:{x}−\mathrm{cos}\:^{\mathrm{3}} {x}}{\mathrm{1}−\mathrm{cos}\:^{\mathrm{3}} {x}}}\:. \\ $$
Answered by MJS last updated on 10/Jun/18
∫(√((cos x −cos^3 x)/(1−cos^3 x)))dx=∫((sin x (√(cos x)))/( (√(1−cos^3 x))))= [t=(√(cos^3 x)) → dx=−((2dt)/(3sin x (√(cos x))))] =−(2/3)∫(dt/( (√(1−t^2 ))))=−(2/3)arcsin t= =−(2/3)arcsin (√(cos^3 x))+C
$$\int\sqrt{\frac{\mathrm{cos}\:{x}\:−\mathrm{cos}^{\mathrm{3}} \:{x}}{\mathrm{1}−\mathrm{cos}^{\mathrm{3}} \:{x}}}{dx}=\int\frac{\mathrm{sin}\:{x}\:\sqrt{\mathrm{cos}\:{x}}}{\:\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{3}} \:{x}}}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\sqrt{\mathrm{cos}^{\mathrm{3}} \:{x}}\:\rightarrow\:{dx}=−\frac{\mathrm{2}{dt}}{\mathrm{3sin}\:{x}\:\sqrt{\mathrm{cos}\:{x}}}\right] \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:{t}= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arcsin}\:\sqrt{\mathrm{cos}^{\mathrm{3}} \:{x}}+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *