Question Number 53522 by 0955083339 last updated on 22/Jan/19

$$\mathrm{Cost}\:\mathrm{of}\:\:\mathrm{2}\:\mathrm{pencils}\:\mathrm{and}\:\:\mathrm{3}\:\mathrm{erasers}\:\mathrm{is}\:\mathrm{Rs}.\mathrm{18}, \\ $$$$\mathrm{while}\:\mathrm{the}\:\mathrm{cost}\:\mathrm{of}\:\:\mathrm{1}\:\:\mathrm{pencil}\:\mathrm{and}\:\:\mathrm{2}\:\mathrm{erasers} \\ $$$$\mathrm{is}\:\mathrm{Rs}.\:\mathrm{11}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{cost}\:\mathrm{of}\:\mathrm{each}\:\mathrm{pencil}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19
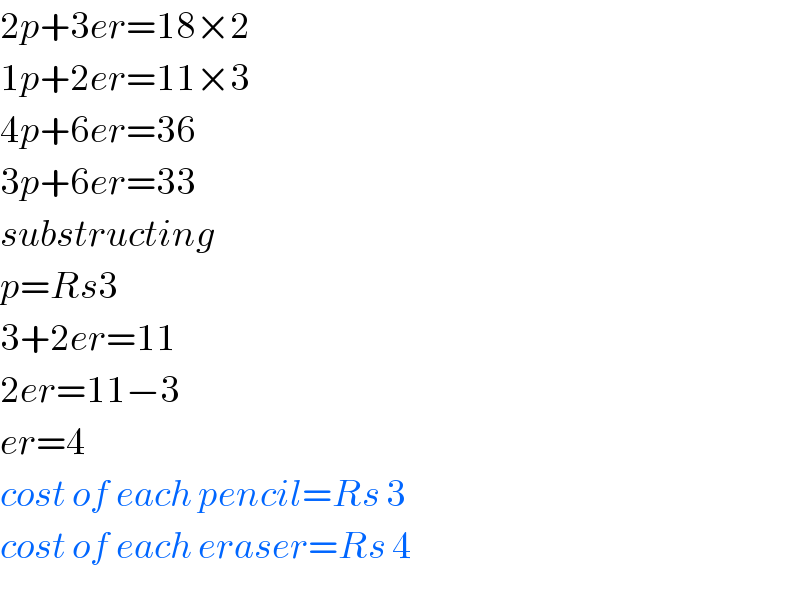
$$\mathrm{2}{p}+\mathrm{3}{er}=\mathrm{18}×\mathrm{2} \\ $$$$\mathrm{1}{p}+\mathrm{2}{er}=\mathrm{11}×\mathrm{3} \\ $$$$\mathrm{4}{p}+\mathrm{6}{er}=\mathrm{36} \\ $$$$\mathrm{3}{p}+\mathrm{6}{er}=\mathrm{33} \\ $$$${substructing} \\ $$$${p}={Rs}\mathrm{3} \\ $$$$\mathrm{3}+\mathrm{2}{er}=\mathrm{11} \\ $$$$\mathrm{2}{er}=\mathrm{11}−\mathrm{3} \\ $$$${er}=\mathrm{4} \\ $$$${cost}\:{of}\:{each}\:{pencil}={Rs}\:\mathrm{3} \\ $$$${cost}\:{of}\:{each}\:{eraser}={Rs}\:\mathrm{4} \\ $$
