Question Number 64327 by Chi Mes Try last updated on 16/Jul/19

$$\frac{{d}}{{dx}}\:\:\left(\:\underset{{f}\left({x}\right)} {\overset{{g}\left({x}\right)} {\int}}\:\phi\left({t}\right)\:{dt}\:\right)\:= \\ $$
Commented by mathmax by abdo last updated on 16/Jul/19
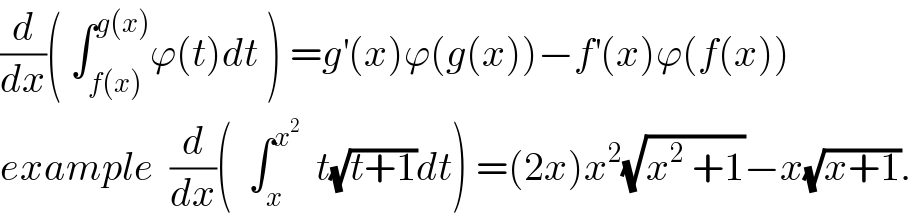
$$\frac{{d}}{{dx}}\left(\:\int_{{f}\left({x}\right)} ^{{g}\left({x}\right)} \varphi\left({t}\right){dt}\:\right)\:={g}^{'} \left({x}\right)\varphi\left({g}\left({x}\right)\right)−{f}^{'} \left({x}\right)\varphi\left({f}\left({x}\right)\right) \\ $$$${example}\:\:\frac{{d}}{{dx}}\left(\:\:\int_{{x}} ^{{x}^{\mathrm{2}} } \:\:{t}\sqrt{{t}+\mathrm{1}}{dt}\right)\:=\left(\mathrm{2}{x}\right){x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}−{x}\sqrt{{x}+\mathrm{1}}. \\ $$
