Question Number 81873 by zainal tanjung last updated on 16/Feb/20
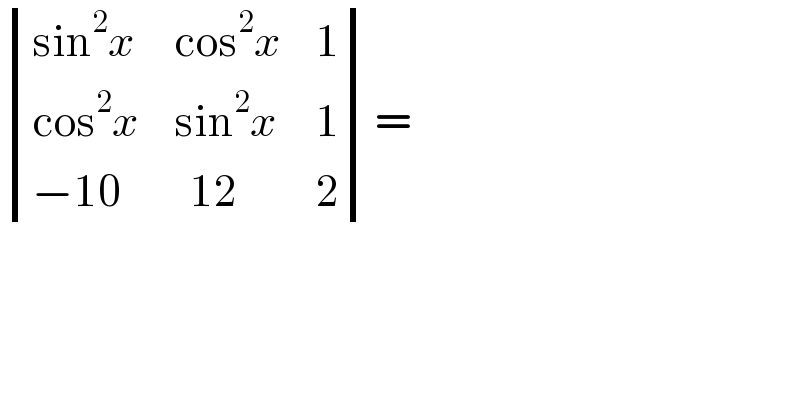
$$\begin{vmatrix}{\mathrm{sin}^{\mathrm{2}} {x}}&{\mathrm{cos}^{\mathrm{2}} {x}}&{\mathrm{1}}\\{\mathrm{cos}^{\mathrm{2}} {x}}&{\mathrm{sin}^{\mathrm{2}} {x}}&{\mathrm{1}}\\{−\mathrm{10}}&{\:\:\mathrm{12}}&{\mathrm{2}}\end{vmatrix}= \\ $$
Commented by john santu last updated on 16/Feb/20
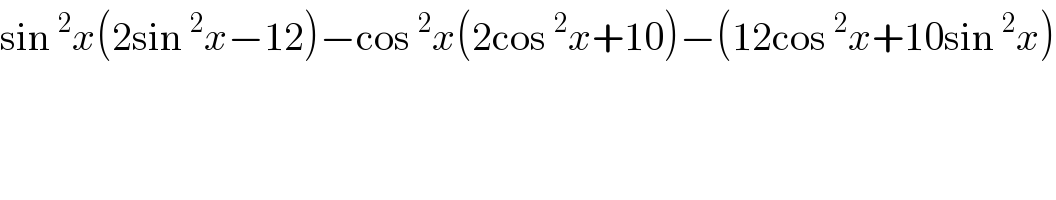
$$\mathrm{sin}\:^{\mathrm{2}} {x}\left(\mathrm{2sin}\:^{\mathrm{2}} {x}−\mathrm{12}\right)−\mathrm{cos}\:^{\mathrm{2}} {x}\left(\mathrm{2cos}\:^{\mathrm{2}} {x}+\mathrm{10}\right)−\left(\mathrm{12cos}\:^{\mathrm{2}} {x}+\mathrm{10sin}\:^{\mathrm{2}} {x}\right) \\ $$
Answered by MJS last updated on 16/Feb/20
![=2(sin^4 x −sin^2 x −cos^4 x +cos^2 x)= [cos x =(√(1−sin^2 x))] =0](https://www.tinkutara.com/question/Q81935.png)
$$=\mathrm{2}\left(\mathrm{sin}^{\mathrm{4}} \:{x}\:−\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{cos}^{\mathrm{2}} \:{x}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{cos}\:{x}\:=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}}\right] \\ $$$$=\mathrm{0} \\ $$
