Question Number 7511 by Obenfo last updated on 01/Sep/16
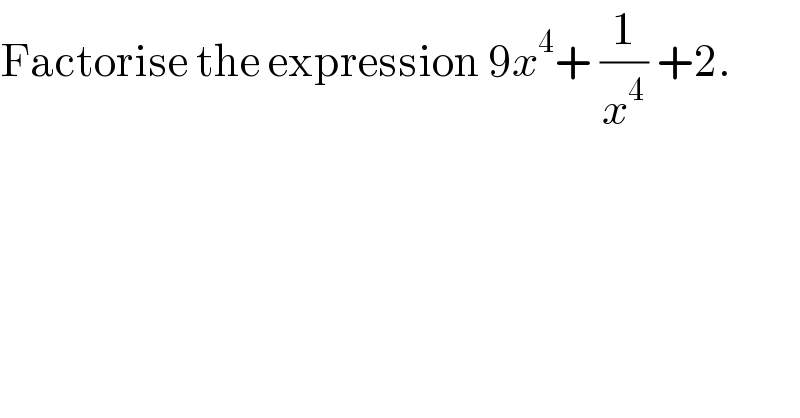
$$\mathrm{Factorise}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{9}{x}^{\mathrm{4}} +\:\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:+\mathrm{2}. \\ $$
Answered by sandy_suhendra last updated on 01/Sep/16
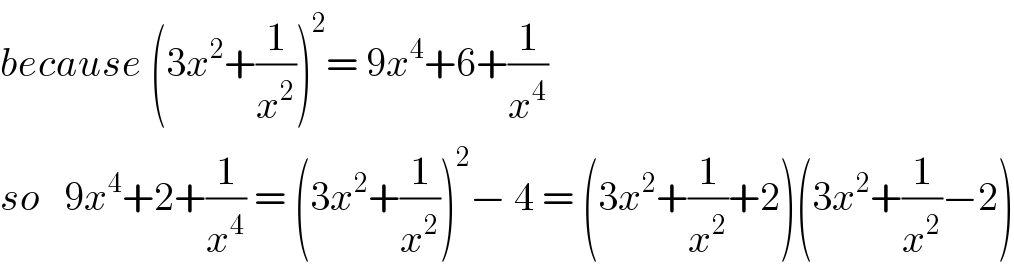
$${because}\:\left(\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\:\mathrm{9}{x}^{\mathrm{4}} +\mathrm{6}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} } \\ $$$${so}\:\:\:\mathrm{9}{x}^{\mathrm{4}} +\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\left(\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\:\mathrm{4}\:=\:\left(\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{2}\right)\left(\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{2}\right) \\ $$
