Question Number 25948 by 272; 2; 2 last updated on 16/Dec/17
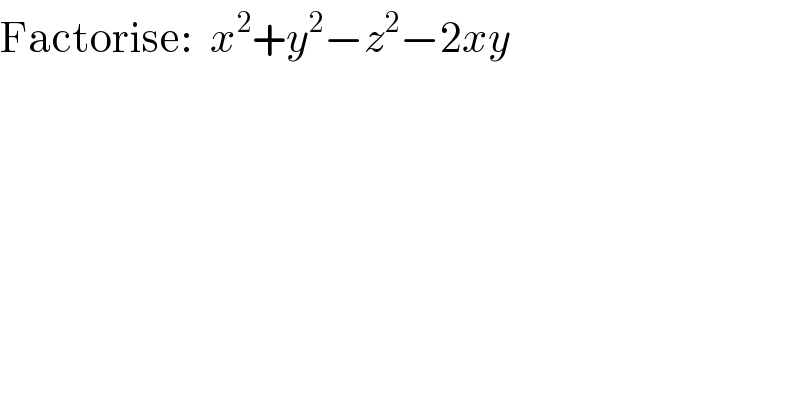
$$\mathrm{Factorise}:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{z}^{\mathrm{2}} −\mathrm{2}{xy} \\ $$
Commented by tawa tawa last updated on 16/Dec/17

$$\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{z}^{\mathrm{2}} \:−\:\mathrm{2xy} \\ $$$$\mathrm{rearrange} \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\mathrm{2xy}\:+\:\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{xy}\:−\:\mathrm{xy}\:+\:\mathrm{y}^{\mathrm{2}} \:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{xy}\right)\:−\:\left(\mathrm{xy}\:+\:\mathrm{y}^{\mathrm{2}} \right)\:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\mathrm{x}\left(\mathrm{x}\:−\:\mathrm{y}\right)\:−\:\mathrm{y}\left(\mathrm{x}\:−\:\mathrm{y}\right)\:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\left(\mathrm{x}\:−\:\mathrm{y}\right)\left(\mathrm{x}\:−\:\mathrm{y}\right)\:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\left(\mathrm{x}\:−\:\mathrm{y}\right)^{\mathrm{2}} \:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$\mathrm{From}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{two}\:\mathrm{square}:\:\:\mathrm{a}^{\mathrm{2}} \:−\:\mathrm{b}^{\mathrm{2}} \:=\:\left(\mathrm{a}\:+\:\mathrm{b}\right)\left(\mathrm{a}\:−\:\mathrm{b}\right) \\ $$$$\mathrm{where},\:\:\mathrm{a}\:=\:\mathrm{x}\:−\:\mathrm{y}\:\:\mathrm{and}\:\:\mathrm{b}\:=\:\mathrm{z} \\ $$$$=\:\left(\mathrm{x}\:−\:\mathrm{y}\right)^{\mathrm{2}} \:−\:\mathrm{z}^{\mathrm{2}} \\ $$$$=\:\left(\mathrm{x}\:−\:\mathrm{y}\:+\:\mathrm{z}\right)\left(\mathrm{x}\:−\:\mathrm{y}\:−\:\mathrm{z}\right) \\ $$
