Question Number 106664 by deep last updated on 06/Aug/20
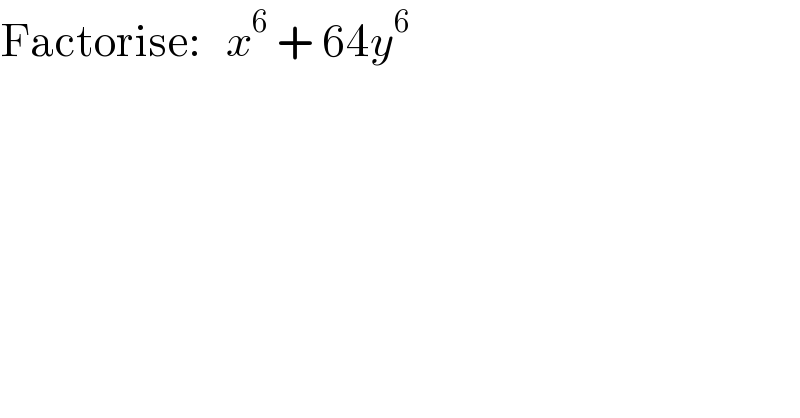
$$\mathrm{Factorise}:\:\:\:{x}^{\mathrm{6}} \:+\:\mathrm{64}{y}^{\mathrm{6}} \\ $$
Answered by som(math1967) last updated on 06/Aug/20
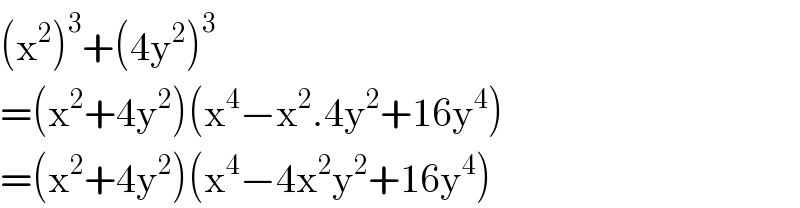
$$\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left(\mathrm{4y}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} .\mathrm{4y}^{\mathrm{2}} +\mathrm{16y}^{\mathrm{4}} \right) \\ $$$$=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{4y}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{4x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} +\mathrm{16y}^{\mathrm{4}} \right) \\ $$
Answered by nimnim last updated on 06/Aug/20
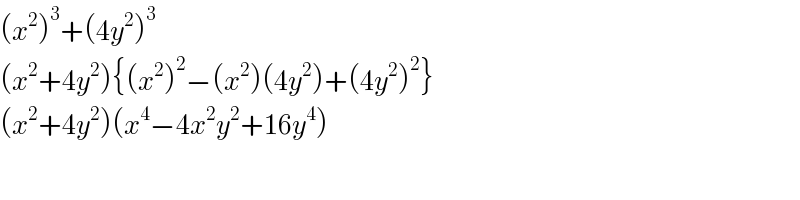
$$\left({x}^{\mathrm{2}} \right)^{\mathrm{3}} +\left(\mathrm{4}{y}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} \right)\left\{\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} \right)\left(\mathrm{4}{y}^{\mathrm{2}} \right)+\left(\mathrm{4}{y}^{\mathrm{2}} \right)^{\mathrm{2}} \right\} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{16}{y}^{\mathrm{4}} \right) \\ $$
Answered by abdomathmax last updated on 07/Aug/20
![let p(x) =x^6 +64y^6 roots of p(x) p(x)=0 ⇔x^6 =−64y^6 ⇒((x/y))^6 =−2^6 ⇒ ((x/(2y)))^6 =−1 =e^(i(2k+1)π) ⇒(x/(2y)) =e^((i(2k+1)π)/6) ⇒the roots are x_k =2y e^((i(2k+1)π)/6) with k∈[[0,5]] ⇒ p(x) =Π_(k=0) ^5 (x−2ye^((i(2k+1)π)/6) )(factorisation atC(x])](https://www.tinkutara.com/question/Q106902.png)
$$\mathrm{let}\:\mathrm{p}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{6}} \:+\mathrm{64y}^{\mathrm{6}} \:\mathrm{roots}\:\mathrm{of}\:\mathrm{p}\left(\mathrm{x}\right) \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\mathrm{0}\:\Leftrightarrow\mathrm{x}^{\mathrm{6}} \:=−\mathrm{64y}^{\mathrm{6}} \:\Rightarrow\left(\frac{\mathrm{x}}{\mathrm{y}}\right)^{\mathrm{6}} \:=−\mathrm{2}^{\mathrm{6}} \:\Rightarrow \\ $$$$\left(\frac{\mathrm{x}}{\mathrm{2y}}\right)^{\mathrm{6}} \:=−\mathrm{1}\:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi} \:\Rightarrow\frac{\mathrm{x}}{\mathrm{2y}}\:=\mathrm{e}^{\frac{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{6}}} \:\Rightarrow\mathrm{the}\:\mathrm{roots}\:\mathrm{are} \\ $$$$\mathrm{x}_{\mathrm{k}} =\mathrm{2y}\:\mathrm{e}^{\frac{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{6}}} \:\:\mathrm{with}\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{5}\right]\right]\:\Rightarrow \\ $$$$\mathrm{p}\left(\mathrm{x}\right)\:=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \left(\mathrm{x}−\mathrm{2ye}^{\frac{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{6}}} \right)\left(\mathrm{factorisation}\:\mathrm{atC}\left(\mathrm{x}\right]\right) \\ $$
