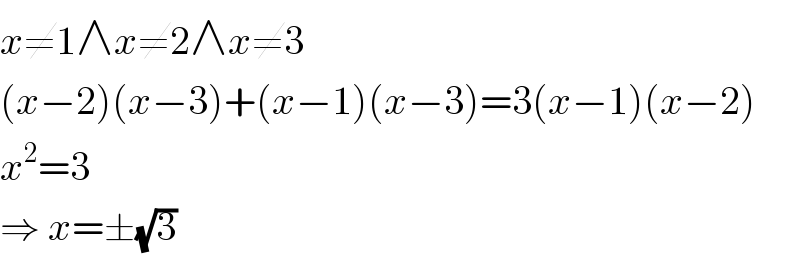Find-the-value-of-x-in-1-x-1-1-x-2-3-x-3-

Question Number 62610 by hovea cw last updated on 23/Jun/19

Find the value of x in

\frac{1}{x - 1} + \frac{1}{x - 2} = \frac{3}{x - 3} .

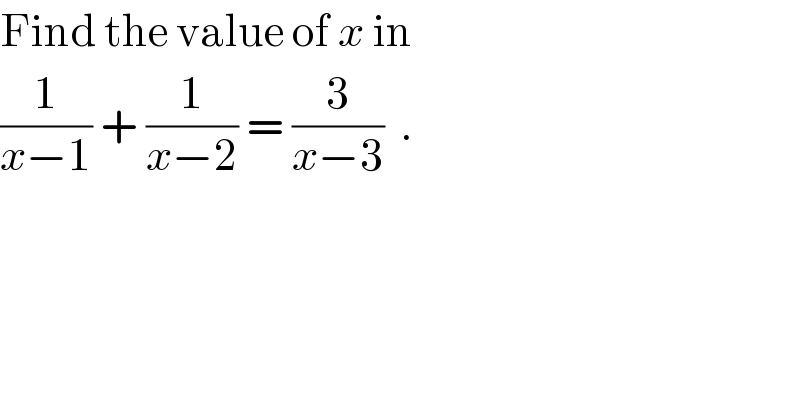
Commented by mathmax by abdo last updated on 24/Jun/19

t h e s e t o f d e f i n i t i o n f o r t h i s (e) i s D = R - {1, 2, 3}

(e) \Leftrightarrow \frac{x - 2 + x - 1}{(x - 1) (x - 2)} = \frac{3}{x - 3} \Rightarrow \frac{2 x - 3}{x^{2} - 3 x + 2} = \frac{3}{x - 3} \Rightarrow

(2 x - 3) (x - 3) = 3 (x^{2} - 3 x + 2) \Rightarrow 2 x^{2} - 6 x - 3 x + 9 = 3 x^{2} - 9 x + 6 \Rightarrow

3 x^{2} - 9 x + 6 - 2 x^{2} + 6 x - 9 = 0 \Rightarrow x^{2} - 3 x - 3 = 0

Δ = 9 - 4 (- 3) = 9 + 12 = 21 \Rightarrow x_{1} = \frac{3 + \sqrt{21}}{2} a n d x_{2} = \frac{3 - \sqrt{21}}{2}

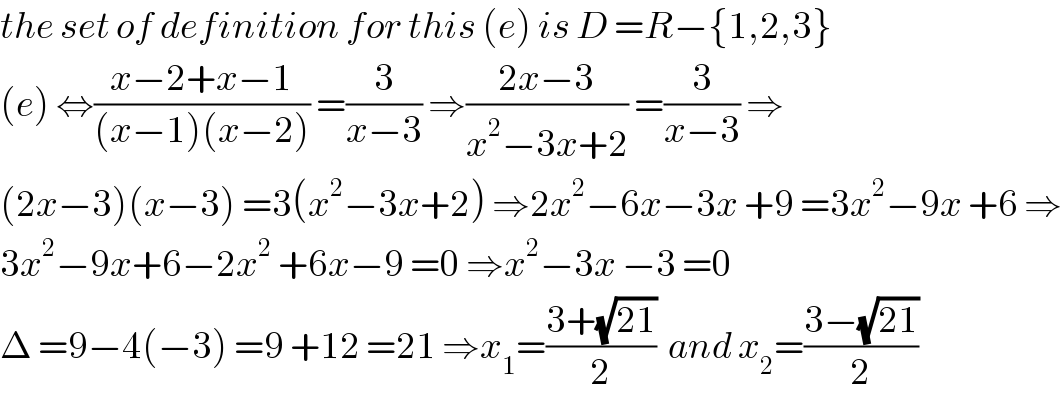
Commented by $@ty@m last updated on 24/Jun/19

P l . c h e c k \dots

3 x^{2} - 9 x + 6 - 2 x^{2} + 6 x - 9 = 0

s h o u l d b e

3 x^{2} - 9 x + 6 - 2 x^{2} + 6 x + 3 x - 9 = 0

Answered by $@ty@m last updated on 23/Jun/19

\frac{1}{x - 1} - \frac{1}{x - 3} = \frac{2}{x - 3} - \frac{1}{x - 2}

\frac{x - 3 - x + 1}{(x - 1) (x - 3)} = \frac{2 x - 4 - x + 3}{(x - 3) (x - 2)}

\frac{- 2}{x - 1} = \frac{x - 1}{x - 2}

- 2 x + 4 = x^{2} - 2 x + 1

x^{2} = 3

x = \sqrt{3}

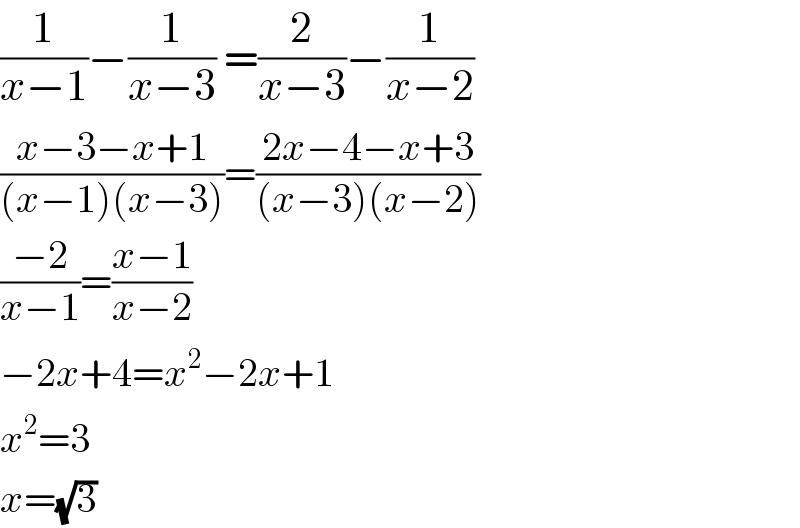
Answered by MJS last updated on 23/Jun/19

x \neq 1 \land x \neq 2 \land x \neq 3

(x - 2) (x - 3) + (x - 1) (x - 3) = 3 (x - 1) (x - 2)

x^{2} = 3

\Rightarrow x = \pm \sqrt{3}

Facebook Tweet Pin