Question Number 81629 by zainal tanjung last updated on 14/Feb/20
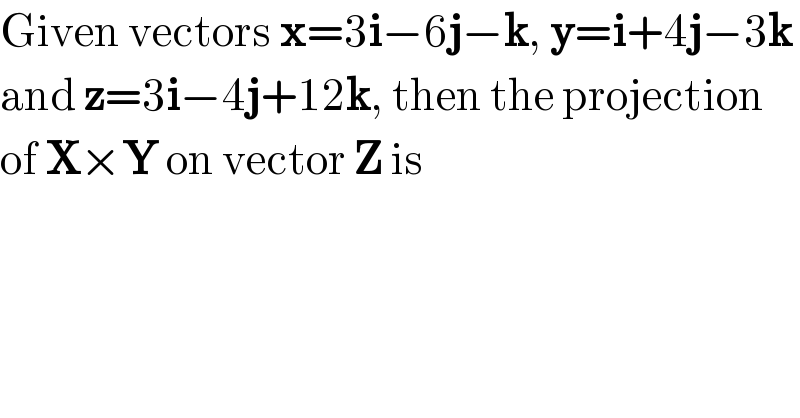
$$\mathrm{Given}\:\mathrm{vectors}\:\boldsymbol{\mathrm{x}}=\mathrm{3}\boldsymbol{\mathrm{i}}−\mathrm{6}\boldsymbol{\mathrm{j}}−\boldsymbol{\mathrm{k}},\:\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{i}}+\mathrm{4}\boldsymbol{\mathrm{j}}−\mathrm{3}\boldsymbol{\mathrm{k}} \\ $$$$\mathrm{and}\:\boldsymbol{\mathrm{z}}=\mathrm{3}\boldsymbol{\mathrm{i}}−\mathrm{4}\boldsymbol{\mathrm{j}}+\mathrm{12}\boldsymbol{\mathrm{k}},\:\mathrm{then}\:\mathrm{the}\:\mathrm{projection} \\ $$$$\mathrm{of}\:\boldsymbol{\mathrm{X}}×\boldsymbol{\mathrm{Y}}\:\mathrm{on}\:\mathrm{vector}\:\boldsymbol{\mathrm{Z}}\:\mathrm{is} \\ $$
Answered by mr W last updated on 14/Feb/20
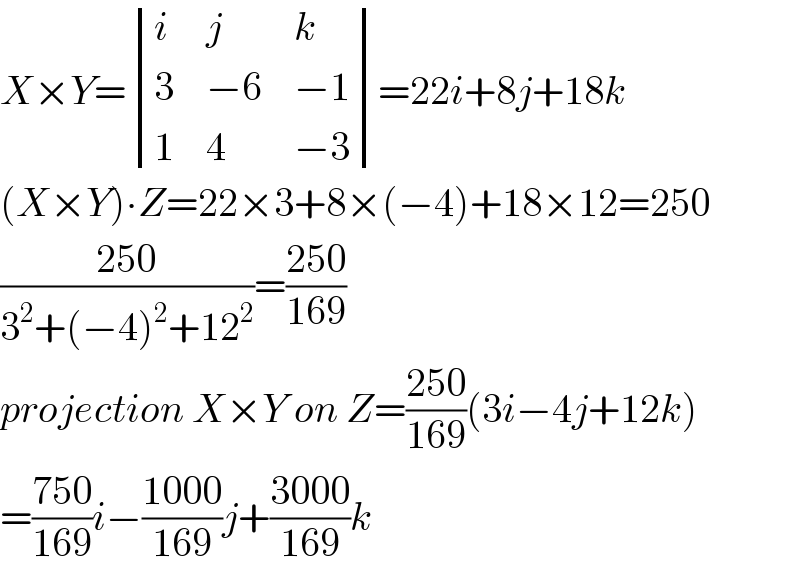
$${X}×{Y}=\begin{vmatrix}{{i}}&{{j}}&{{k}}\\{\mathrm{3}}&{−\mathrm{6}}&{−\mathrm{1}}\\{\mathrm{1}}&{\mathrm{4}}&{−\mathrm{3}}\end{vmatrix}=\mathrm{22}{i}+\mathrm{8}{j}+\mathrm{18}{k} \\ $$$$\left({X}×{Y}\right)\centerdot{Z}=\mathrm{22}×\mathrm{3}+\mathrm{8}×\left(−\mathrm{4}\right)+\mathrm{18}×\mathrm{12}=\mathrm{250} \\ $$$$\frac{\mathrm{250}}{\mathrm{3}^{\mathrm{2}} +\left(−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\frac{\mathrm{250}}{\mathrm{169}} \\ $$$${projection}\:{X}×{Y}\:{on}\:{Z}=\frac{\mathrm{250}}{\mathrm{169}}\left(\mathrm{3}{i}−\mathrm{4}{j}+\mathrm{12}{k}\right) \\ $$$$=\frac{\mathrm{750}}{\mathrm{169}}{i}−\frac{\mathrm{1000}}{\mathrm{169}}{j}+\frac{\mathrm{3000}}{\mathrm{169}}{k} \\ $$
Commented by Zainal Arifin last updated on 14/Feb/20

$$\mathrm{Thanks}\:\mathrm{sir}.. \\ $$
