Menu Close

If-1-4-f-x-dx-4-and-2-4-3-f-x-dx-7-then-2-1-f-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 55526 by alex26 last updated on 26/Feb/19
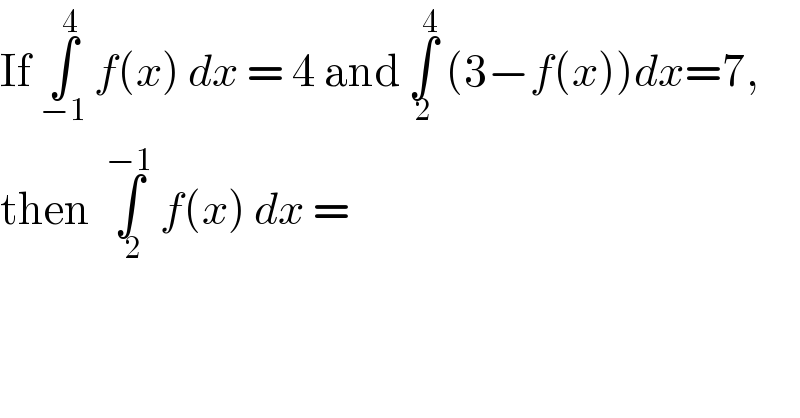
If ∫_(−1) ^4 f(x) dx = 4 and ∫_2 ^4 (3−f(x))dx=7, then ∫_( 2) ^(−1) f(x) dx =
$$\mathrm{If}\:\underset{−\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\mathrm{4}\:\mathrm{and}\:\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:\left(\mathrm{3}−{f}\left({x}\right)\right){dx}=\mathrm{7}, \\ $$$$\mathrm{then}\:\:\underset{\:\mathrm{2}} {\overset{−\mathrm{1}} {\int}}\:{f}\left({x}\right)\:{dx}\:= \\ $$
Commented by mr W last updated on 26/Feb/19
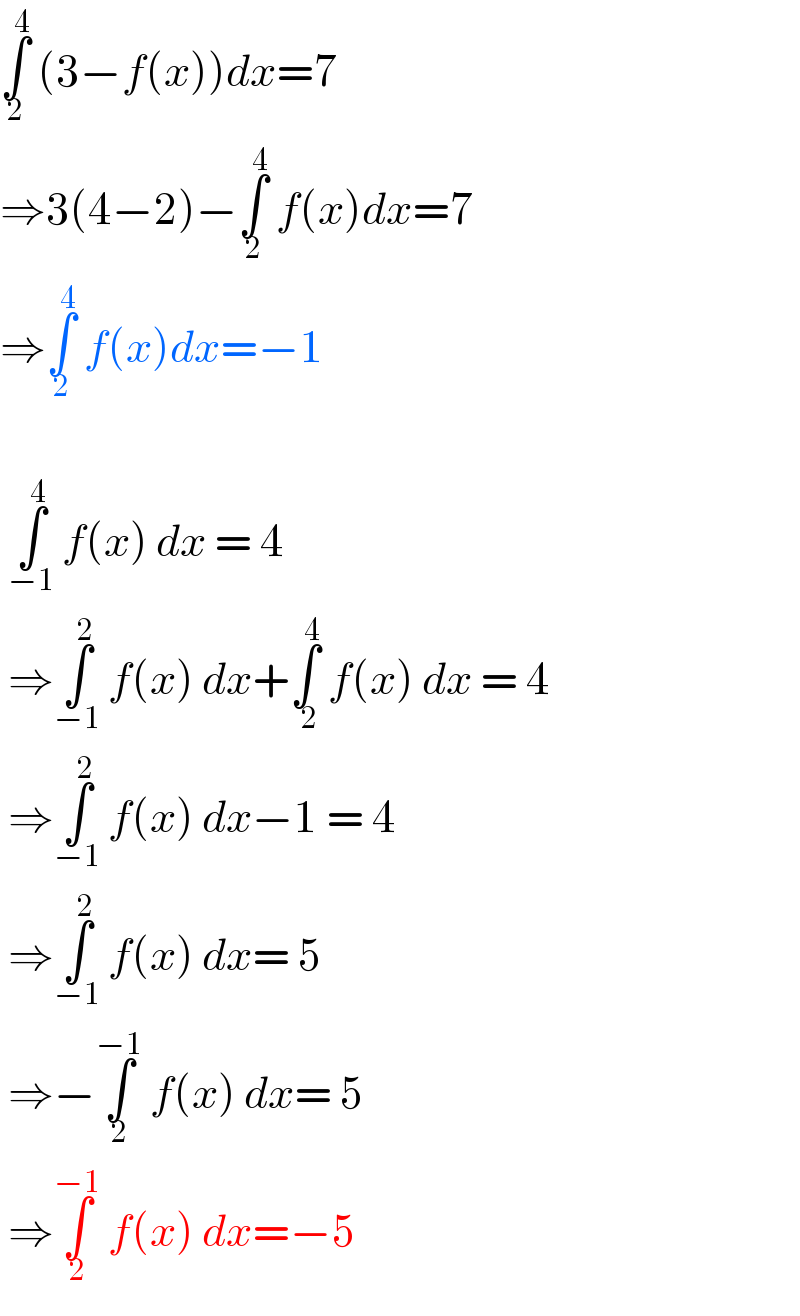
∫_2 ^4 (3−f(x))dx=7 ⇒3(4−2)−∫_2 ^4 f(x)dx=7 ⇒∫_2 ^4 f(x)dx=−1 ∫_(−1) ^4 f(x) dx = 4 ⇒∫_(−1) ^2 f(x) dx+∫_( 2) ^4 f(x) dx = 4 ⇒∫_(−1) ^2 f(x) dx−1 = 4 ⇒∫_(−1) ^2 f(x) dx= 5 ⇒−∫_2 ^(−1) f(x) dx= 5 ⇒∫_2 ^(−1) f(x) dx=−5
$$\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:\left(\mathrm{3}−{f}\left({x}\right)\right){dx}=\mathrm{7} \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{4}−\mathrm{2}\right)−\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right){dx}=\mathrm{7} \\ $$$$\Rightarrow\underset{\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right){dx}=−\mathrm{1} \\ $$$$ \\ $$$$\:\underset{−\mathrm{1}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\mathrm{4} \\ $$$$\:\Rightarrow\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right)\:{dx}+\underset{\:\mathrm{2}} {\overset{\mathrm{4}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\mathrm{4} \\ $$$$\:\Rightarrow\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right)\:{dx}−\mathrm{1}\:=\:\mathrm{4} \\ $$$$\:\Rightarrow\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\:{f}\left({x}\right)\:{dx}=\:\mathrm{5} \\ $$$$\:\Rightarrow−\underset{\mathrm{2}} {\overset{−\mathrm{1}} {\int}}\:{f}\left({x}\right)\:{dx}=\:\mathrm{5} \\ $$$$\:\Rightarrow\underset{\mathrm{2}} {\overset{−\mathrm{1}} {\int}}\:{f}\left({x}\right)\:{dx}=−\mathrm{5} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Feb/19
∫f(x)dx=g(x)+c ∫_(−1) ^4 f(x)dx g(4)−g(−1)=4.....(1)eqn ∫_2 ^4 {3−f(x)}dx ∣3x−g(x)∣_2 ^4 3×4−g(4)−3×2+g(2) 6−g(4)+g(2)=7.....(2)eqn add eqn1 and ean 2 6+g(2)−g(−1)=11 g(2)−g(−1)=5 g(−1)−g(2)=−5 so ∫_2 ^(−1) f(x)dx=−5 pls check...
$$\int{f}\left({x}\right){dx}={g}\left({x}\right)+{c} \\ $$$$\int_{−\mathrm{1}} ^{\mathrm{4}} {f}\left({x}\right){dx} \\ $$$${g}\left(\mathrm{4}\right)−{g}\left(−\mathrm{1}\right)=\mathrm{4}…..\left(\mathrm{1}\right){eqn} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{4}} \left\{\mathrm{3}−{f}\left({x}\right)\right\}{dx} \\ $$$$\mid\mathrm{3}{x}−{g}\left({x}\right)\mid_{\mathrm{2}} ^{\mathrm{4}} \\ $$$$\mathrm{3}×\mathrm{4}−{g}\left(\mathrm{4}\right)−\mathrm{3}×\mathrm{2}+{g}\left(\mathrm{2}\right) \\ $$$$\mathrm{6}−{g}\left(\mathrm{4}\right)+{g}\left(\mathrm{2}\right)=\mathrm{7}…..\left(\mathrm{2}\right){eqn} \\ $$$${add}\:{eqn}\mathrm{1}\:{and}\:{ean}\:\mathrm{2} \\ $$$$\mathrm{6}+{g}\left(\mathrm{2}\right)−{g}\left(−\mathrm{1}\right)=\mathrm{11} \\ $$$${g}\left(\mathrm{2}\right)−{g}\left(−\mathrm{1}\right)=\mathrm{5} \\ $$$${g}\left(−\mathrm{1}\right)−{g}\left(\mathrm{2}\right)=−\mathrm{5} \\ $$$${so}\:\int_{\mathrm{2}} ^{−\mathrm{1}} {f}\left({x}\right){dx}=−\mathrm{5} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *