Question Number 62591 by hovea cw last updated on 23/Jun/19
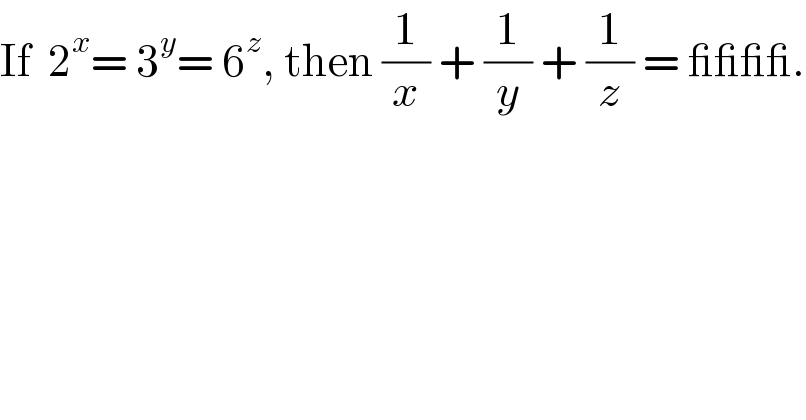
$$\mathrm{If}\:\:\mathrm{2}^{{x}} =\:\mathrm{3}^{{y}} =\:\mathrm{6}^{{z}} ,\:\mathrm{then}\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}\:+\:\frac{\mathrm{1}}{{z}}\:=\:\_\_\_\_. \\ $$
Commented by mr W last updated on 23/Jun/19
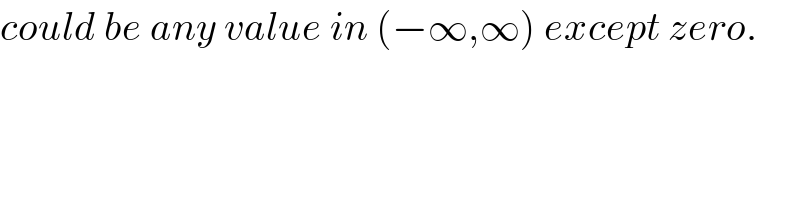
$${could}\:{be}\:{any}\:{value}\:{in}\:\left(−\infty,\infty\right)\:{except}\:{zero}. \\ $$
Answered by MJS last updated on 23/Jun/19
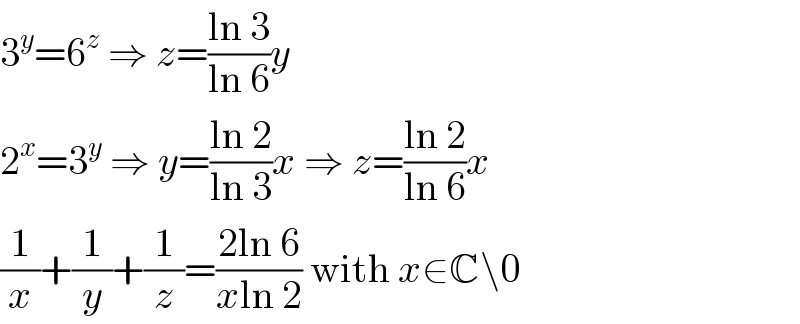
$$\mathrm{3}^{{y}} =\mathrm{6}^{{z}} \:\Rightarrow\:{z}=\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{6}}{y} \\ $$$$\mathrm{2}^{{x}} =\mathrm{3}^{{y}} \:\Rightarrow\:{y}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}{x}\:\Rightarrow\:{z}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\mathrm{6}}{x} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{2ln}\:\mathrm{6}}{{x}\mathrm{ln}\:\mathrm{2}}\:\mathrm{with}\:{x}\in\mathbb{C}\backslash\mathrm{0} \\ $$
Answered by $@ty@m last updated on 23/Jun/19
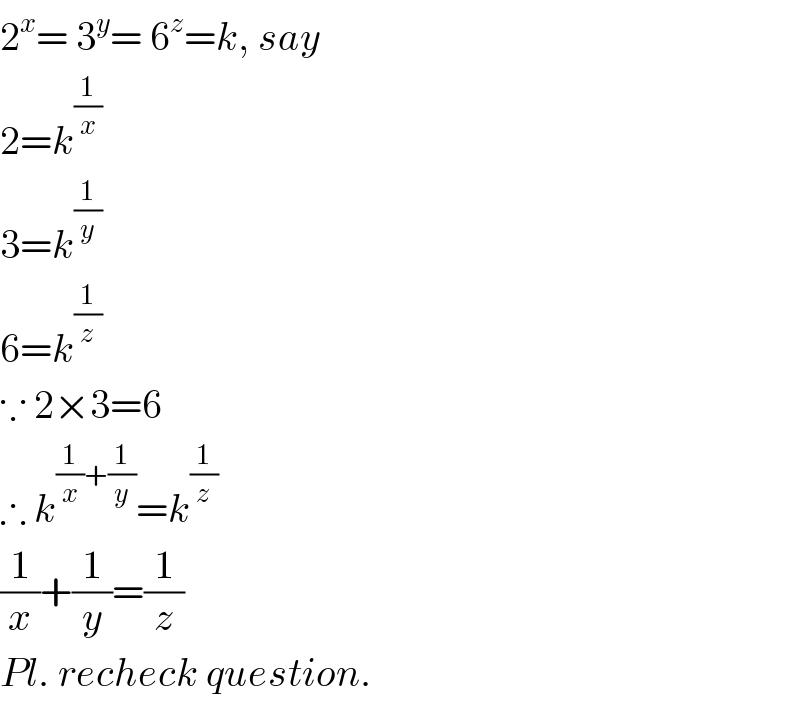
$$\mathrm{2}^{{x}} =\:\mathrm{3}^{{y}} =\:\mathrm{6}^{{z}} ={k},\:{say} \\ $$$$\mathrm{2}={k}^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{3}={k}^{\frac{\mathrm{1}}{{y}}} \\ $$$$\mathrm{6}={k}^{\frac{\mathrm{1}}{{z}}} \\ $$$$\because\:\mathrm{2}×\mathrm{3}=\mathrm{6} \\ $$$$\therefore\:{k}^{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}} ={k}^{\frac{\mathrm{1}}{{z}}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{{z}} \\ $$$${Pl}.\:{recheck}\:{question}. \\ $$
Commented by Tony Lin last updated on 23/Jun/19
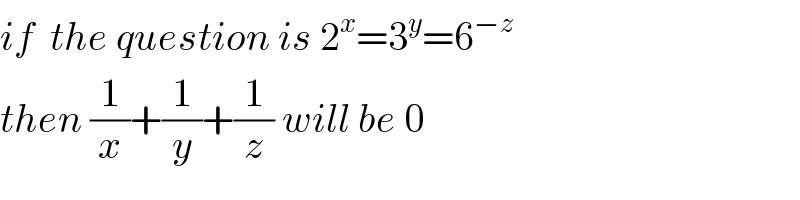
$${if}\:\:{the}\:{question}\:{is}\:\mathrm{2}^{{x}} =\mathrm{3}^{{y}} =\mathrm{6}^{−{z}} \\ $$$${then}\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\:{will}\:{be}\:\mathrm{0} \\ $$
