Question Number 53324 by 0955083339 last updated on 20/Jan/19
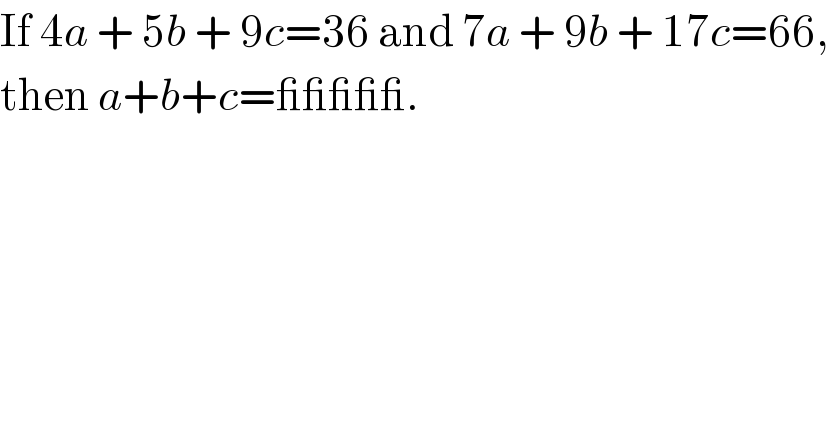
$$\mathrm{If}\:\mathrm{4}{a}\:+\:\mathrm{5}{b}\:+\:\mathrm{9}{c}=\mathrm{36}\:\mathrm{and}\:\mathrm{7}{a}\:+\:\mathrm{9}{b}\:+\:\mathrm{17}{c}=\mathrm{66}, \\ $$$$\mathrm{then}\:{a}+{b}+{c}=\_\_\_\_\_. \\ $$
Answered by Kunal12588 last updated on 21/Jan/19
![let a+b+c=k 4a+4b+4c+b+5c=36 ⇒4k+(b+5c)=36 (1) 7a+7b+7c+2b+10c=66 ⇒7k+2(b+5c)=66 (2) let b+5c=h 4k+h=36 [multiply by 2] 8k+2h=72 7k+2h=66 ⇒k=a+b+c=72−66=6](https://www.tinkutara.com/question/Q53327.png)
$${let}\:{a}+{b}+{c}={k} \\ $$$$\mathrm{4}{a}+\mathrm{4}{b}+\mathrm{4}{c}+{b}+\mathrm{5}{c}=\mathrm{36} \\ $$$$\Rightarrow\mathrm{4}{k}+\left({b}+\mathrm{5}{c}\right)=\mathrm{36}\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{7}{a}+\mathrm{7}{b}+\mathrm{7}{c}+\mathrm{2}{b}+\mathrm{10}{c}=\mathrm{66} \\ $$$$\Rightarrow\mathrm{7}{k}+\mathrm{2}\left({b}+\mathrm{5}{c}\right)=\mathrm{66}\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:\:\: \\ $$$${let}\:{b}+\mathrm{5}{c}={h} \\ $$$$\mathrm{4}{k}+{h}=\mathrm{36}\:\:\:\:\left[{multiply}\:{by}\:\mathrm{2}\right] \\ $$$$\mathrm{8}{k}+\mathrm{2}{h}=\mathrm{72} \\ $$$$\mathrm{7}{k}+\mathrm{2}{h}=\mathrm{66} \\ $$$$\Rightarrow{k}={a}+{b}+{c}=\mathrm{72}−\mathrm{66}=\mathrm{6} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 21/Jan/19

$${excellent}… \\ $$
