Menu Close

If-a-2-a-C-2-a-2-a-C-4-then-a-

Tinku Tara 0 Comments
Pin




Question Number 97737 by bagjamath last updated on 09/Jun/20
If ^((a^2 −a)) C_2 =^((a^2 −a)) C_4 , then a =
If(a2−a)C2=(a2−a)C4,thena=
Commented by som(math1967) last updated on 09/Jun/20
a=3
a=3
Commented by smridha last updated on 09/Jun/20
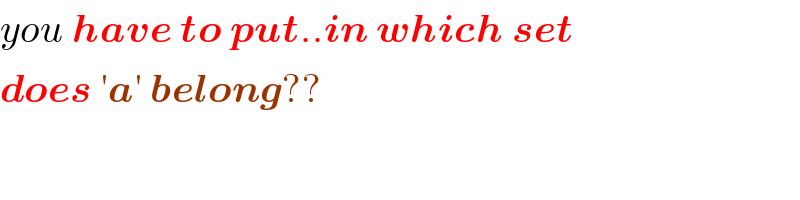
you have to put..in which set does ′a′ belong??
youhavetoput..inwhichsetdoes′a′belong??
Commented by mr W last updated on 09/Jun/20
a^2 −a=2+4=6 (a+2)(a−3)=0 ⇒a=3
a2−a=2+4=6(a+2)(a−3)=0⇒a=3
Answered by smridha last updated on 09/Jun/20
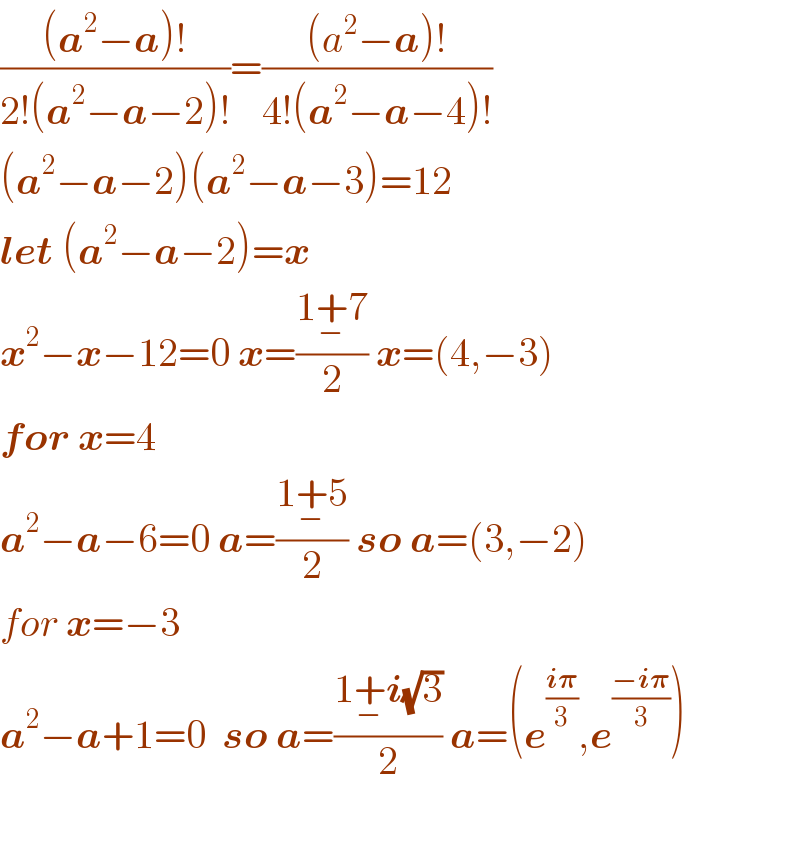
(((a^2 −a)!)/(2!(a^2 −a−2)!))=(((a^2 −a)!)/(4!(a^2 −a−4)!)) (a^2 −a−2)(a^2 −a−3)=12 let (a^2 −a−2)=x x^2 −x−12=0 x=((1+_− 7)/2) x=(4,−3) for x=4 a^2 −a−6=0 a=((1+_− 5)/2) so a=(3,−2) for x=−3 a^2 −a+1=0 so a=((1+_− i(√3))/2) a=(e^((i𝛑)/3) ,e^((−i𝛑)/3) )
(a2−a)!2!(a2−a−2)!=(a2−a)!4!(a2−a−4)!(a2−a−2)(a2−a−3)=12let(a2−a−2)=xx2−x−12=0x=1+−72x=(4,−3)forx=4a2−a−6=0a=1+−52soa=(3,−2)forx=−3a2−a+1=0soa=1+−i32a=(eiπ3,e−iπ3)
Commented by smridha last updated on 09/Jun/20
I am not fighting with others... but you tried to do so I think.. I just wanted to tell two simple things (i)I am not claim all the possible values of a are the solutions(ii) even I didnot conclude anything so why you are the guys are so worrid with that... am I criticize anyone??if this is so simple matter then it is not requare furthur comment.
Iamnotfightingwithothers…butyoutriedtodosoIthink..Ijustwantedtotelltwosimplethings(i)Iamnotclaimallthepossiblevaluesofaarethesolutions(ii)evenIdidnotconcludeanythingsowhyyouaretheguysaresoworridwiththat…amIcriticizeanyone??ifthisissosimplematterthenitisnotrequarefurthurcomment.
Commented by mathmax by abdo last updated on 09/Jun/20
how to get complex number in combination...!
howtogetcomplexnumberincombination…!
Commented by smridha last updated on 09/Jun/20
am I put complex number in combination???then what?? I just show how many values a have??I don′t claim all the possible values must satisfy the combination...... the apperence of this question is wrong!!! find a???what does it mean??we logically choose the value of a among the values of a.so it does not mean that a have only possible value 3.. moreover it means a takes value 3 for satisfy this combination. for this combination 3 is unique value (of a) but not for a.
amIputcomplexnumberincombination???thenwhat??Ijustshowhowmanyvaluesahave??Idon′tclaimallthepossiblevaluesmustsatisfythecombination……theapperenceofthisquestioniswrong!!!finda???whatdoesitmean??welogicallychoosethevalueofaamongthevaluesofa.soitdoesnotmeanthatahaveonlypossiblevalue3..moreoveritmeansatakesvalue3forsatisfythiscombination.forthiscombination3isuniquevalue(ofa)butnotfora.
Commented by mr W last updated on 09/Jun/20
as for the answer of this question, the only correct answer is a=3, other values of a are non−sense for this question. i think as C_2 ^(a^2 −a) =C_4 ^(a^2 −a) is written, it is automatically said due to definition that a∈Z and a^2 −a≥2 and a^2 −a≥4.
asfortheanswerofthisquestion,theonlycorrectanswerisa=3,othervaluesofaarenon−senseforthisquestion.ithinkasC2a2−a=C4a2−aiswritten,itisautomaticallysaidduetodefinitionthata∈Zanda2−a⩾2anda2−a⩾4.
Commented by smridha last updated on 09/Jun/20
ooh man!!am i claim all the possible values satisfy this combination?? even am I put any conclution in my solution?? this is the question of how much we can do?? we have any idea??about the factorial of complex number!! factorial of negetive intiger!! so we ignore them....this is the fault.if there is theory behind them we are then satisfied..is not it????
oohman!!amiclaimallthepossiblevaluessatisfythiscombination??evenamIputanyconclutioninmysolution??thisisthequestionofhowmuchwecando??wehaveanyidea??aboutthefactorialofcomplexnumber!!factorialofnegetiveintiger!!soweignorethem….thisisthefault.ifthereistheorybehindthemwearethensatisfied..isnotit????
Commented by mr W last updated on 09/Jun/20
sir: nobody said that you are wrong or something like that. it seems you see critical comments from others as attacks and want to fight back. what a pity! since a forum is place for discussion,exchange and learning from each other. all people here are equal.
sir:nobodysaidthatyouarewrongorsomethinglikethat.itseemsyouseecriticalcommentsfromothersasattacksandwanttofightback.whatapity!sinceaforumisplacefordiscussion,exchangeandlearningfromeachother.allpeoplehereareequal.
Commented by abdomathmax last updated on 09/Jun/20
your answer is not correct
youranswerisnotcorrect
Commented by smridha last updated on 09/Jun/20
Mr Abdomathmax :am I write any values as ans?? if you think that this is your fult not mine..!!
MrAbdomathmax:amIwriteanyvaluesasans??ifyouthinkthatthisisyourfultnotmine..!!
Commented by mathmax by abdo last updated on 09/Jun/20
dont worry and be happy we are here to help and learn...maths is a sea without borders....!
dontworryandbehappyweareheretohelpandlearn…mathsisaseawithoutborders….!
Answered by mathmax by abdo last updated on 09/Jun/20
C_(a^2 −a) ^2 =C_(a^2 −a) ^4 ⇒(((a^2 −a)!)/(2!(a^2 −a−2)!)) =(((a^2 −a)!)/(4!(a^2 −a−4)!)) (a≥2) ⇒ 2!(a^2 −a−2)! =4! (a^2 −a−4)! ⇒ 2(a^2 −a−2)(a^2 −a−3) =4! ⇒(a^2 −a−2)(a^2 −a−3) =((4.3.2)/2) =12 let a^2 −a−2 =2u and a^2 −a−3 =2v+1 ⇒2v +1 =2u−1 ⇒ 2u.(2v+1) =12 ⇒u(2u−1) =6 ⇒2u^2 −u−6 =0 (u integr natural) Δ =1−4×2×(−6) =1+48 =49 ⇒u_1 =((1+7)/4) =2 u_2 =((1−7)/4) =−(3/2)(to elminate) ⇒u=2 ⇒a^2 −a =2+4 =6 ⇒a^2 −a−6 =0 Δ=1−4(−6) =25 ⇒a =((1+5)/2) =3 or a =((1−5)/2) =−2<0(to eliminate) the unique value is a =3
Ca2−a2=Ca2−a4⇒(a2−a)!2!(a2−a−2)!=(a2−a)!4!(a2−a−4)!(a⩾2)⇒2!(a2−a−2)!=4!(a2−a−4)!⇒2(a2−a−2)(a2−a−3)=4!⇒(a2−a−2)(a2−a−3)=4.3.22=12leta2−a−2=2uanda2−a−3=2v+1⇒2v+1=2u−1⇒2u.(2v+1)=12⇒u(2u−1)=6⇒2u2−u−6=0(uintegrnatural)Δ=1−4×2×(−6)=1+48=49⇒u1=1+74=2u2=1−74=−32(toelminate)⇒u=2⇒a2−a=2+4=6⇒a2−a−6=0Δ=1−4(−6)=25⇒a=1+52=3ora=1−52=−2<0(toeliminate)theuniquevalueisa=3

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *