Menu Close

If-are-the-roots-of-the-equation-ax-2-bx-c-0-then-the-value-of-the-determinant-determinant-1-cos-cos-cos-1-cos-cos-cos-1-is-

Tinku Tara 0 Comments
Pin




Question Number 41820 by v tfvhjdxf last updated on 13/Aug/18
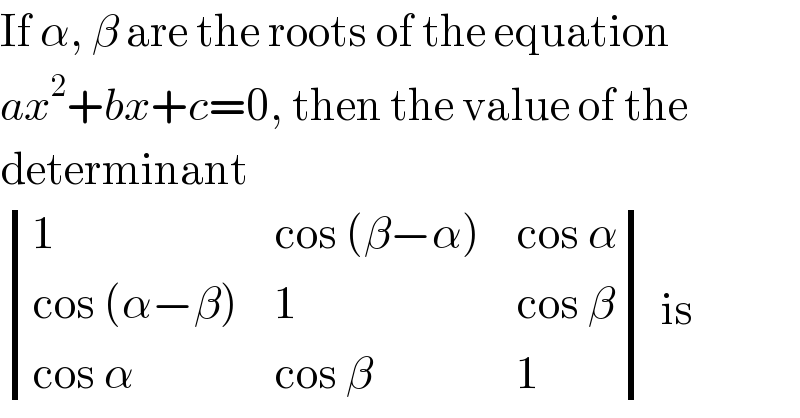
If α, β are the roots of the equation ax^2 +bx+c=0, then the value of the determinant determinant ((1,(cos (β−α)),(cos α)),((cos (α−β)),1,(cos β)),((cos α),(cos β),1)) is
$$\mathrm{If}\:\alpha,\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0},\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{determinant} \\ $$$$\begin{vmatrix}{\mathrm{1}}&{\mathrm{cos}\:\left(\beta−\alpha\right)}&{\mathrm{cos}\:\alpha}\\{\mathrm{cos}\:\left(\alpha−\beta\right)}&{\mathrm{1}}&{\mathrm{cos}\:\beta}\\{\mathrm{cos}\:\alpha}&{\mathrm{cos}\:\beta}&{\mathrm{1}}\end{vmatrix}\:\mathrm{is} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Aug/18
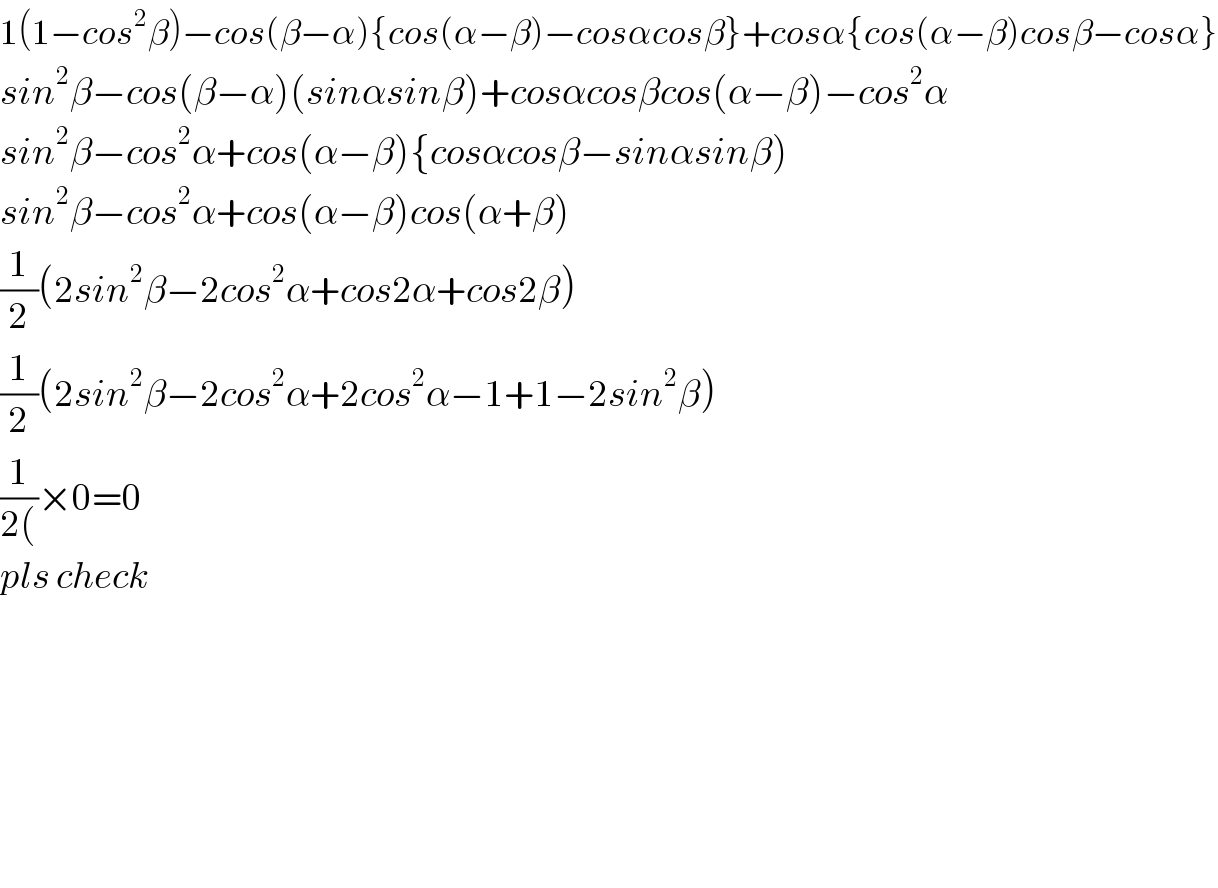
1(1−cos^2 β)−cos(β−α){cos(α−β)−cosαcosβ}+cosα{cos(α−β)cosβ−cosα} sin^2 β−cos(β−α)(sinαsinβ)+cosαcosβcos(α−β)−cos^2 α sin^2 β−cos^2 α+cos(α−β){cosαcosβ−sinαsinβ) sin^2 β−cos^2 α+cos(α−β)cos(α+β) (1/2)(2sin^2 β−2cos^2 α+cos2α+cos2β) (1/2)(2sin^2 β−2cos^2 α+2cos^2 α−1+1−2sin^2 β) (1/(2())×0=0 pls check
$$\mathrm{1}\left(\mathrm{1}−{cos}^{\mathrm{2}} \beta\right)−{cos}\left(\beta−\alpha\right)\left\{{cos}\left(\alpha−\beta\right)−{cos}\alpha{cos}\beta\right\}+{cos}\alpha\left\{{cos}\left(\alpha−\beta\right){cos}\beta−{cos}\alpha\right\} \\ $$$${sin}^{\mathrm{2}} \beta−{cos}\left(\beta−\alpha\right)\left({sin}\alpha{sin}\beta\right)+{cos}\alpha{cos}\beta{cos}\left(\alpha−\beta\right)−{cos}^{\mathrm{2}} \alpha \\ $$$${sin}^{\mathrm{2}} \beta−{cos}^{\mathrm{2}} \alpha+{cos}\left(\alpha−\beta\right)\left\{{cos}\alpha{cos}\beta−{sin}\alpha{sin}\beta\right) \\ $$$${sin}^{\mathrm{2}} \beta−{cos}^{\mathrm{2}} \alpha+{cos}\left(\alpha−\beta\right){cos}\left(\alpha+\beta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{sin}^{\mathrm{2}} \beta−\mathrm{2}{cos}^{\mathrm{2}} \alpha+{cos}\mathrm{2}\alpha+{cos}\mathrm{2}\beta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{sin}^{\mathrm{2}} \beta−\mathrm{2}{cos}^{\mathrm{2}} \alpha+\mathrm{2}{cos}^{\mathrm{2}} \alpha−\mathrm{1}+\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \beta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left(\right.}×\mathrm{0}=\mathrm{0} \\ $$$${pls}\:{check} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *