Question Number 103155 by 9027201563 last updated on 13/Jul/20
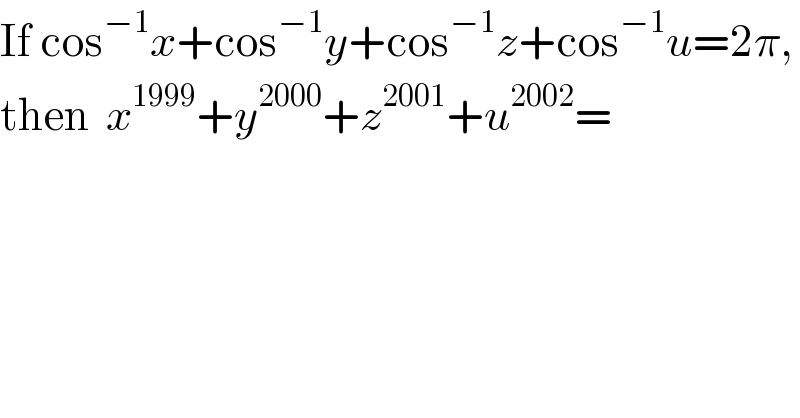
$$\mathrm{If}\:\mathrm{cos}^{−\mathrm{1}} {x}+\mathrm{cos}^{−\mathrm{1}} {y}+\mathrm{cos}^{−\mathrm{1}} {z}+\mathrm{cos}^{−\mathrm{1}} {u}=\mathrm{2}\pi, \\ $$$$\mathrm{then}\:\:{x}^{\mathrm{1999}} +{y}^{\mathrm{2000}} +{z}^{\mathrm{2001}} +{u}^{\mathrm{2002}} = \\ $$
Commented by 9027201563 last updated on 13/Jul/20
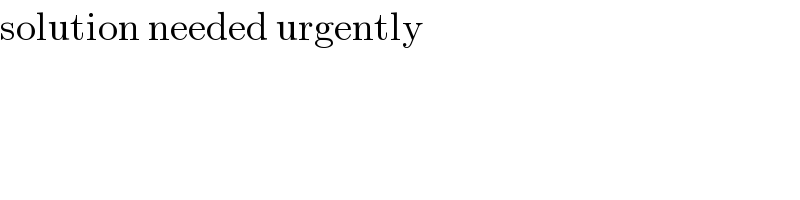
$$\mathrm{solution}\:\mathrm{needed}\:\mathrm{urgently} \\ $$
Commented by prakash jain last updated on 13/Jul/20
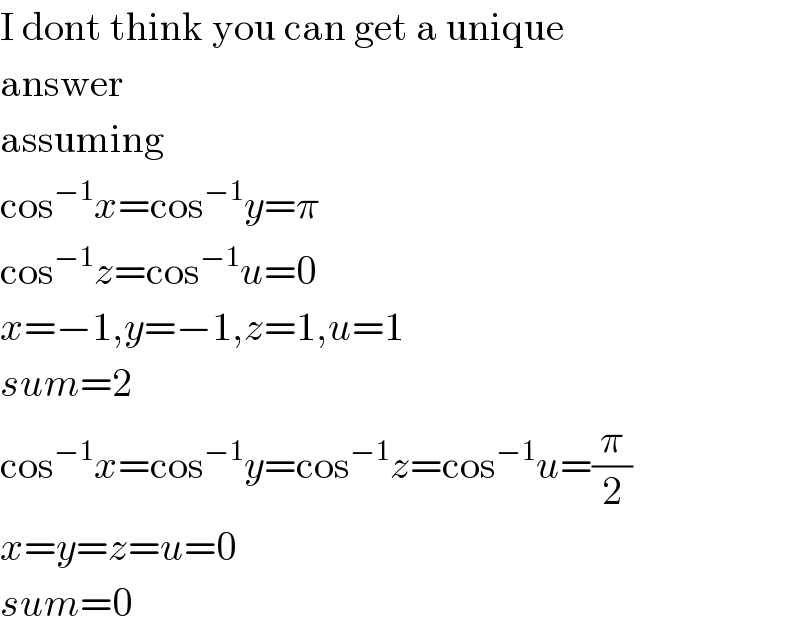
$$\mathrm{I}\:\mathrm{dont}\:\mathrm{think}\:\mathrm{you}\:\mathrm{can}\:\mathrm{get}\:\mathrm{a}\:\mathrm{unique} \\ $$$$\mathrm{answer} \\ $$$$\mathrm{assuming} \\ $$$$\mathrm{cos}^{−\mathrm{1}} {x}=\mathrm{cos}^{−\mathrm{1}} {y}=\pi \\ $$$$\mathrm{cos}^{−\mathrm{1}} {z}=\mathrm{cos}^{−\mathrm{1}} {u}=\mathrm{0} \\ $$$${x}=−\mathrm{1},{y}=−\mathrm{1},{z}=\mathrm{1},{u}=\mathrm{1} \\ $$$${sum}=\mathrm{2} \\ $$$$\mathrm{cos}^{−\mathrm{1}} {x}=\mathrm{cos}^{−\mathrm{1}} {y}=\mathrm{cos}^{−\mathrm{1}} {z}=\mathrm{cos}^{−\mathrm{1}} {u}=\frac{\pi}{\mathrm{2}} \\ $$$${x}={y}={z}={u}=\mathrm{0} \\ $$$${sum}=\mathrm{0} \\ $$
