If-cos-cos-0-sin-sin-then-cos-2-cos-2-

Question Number 97657 by Vishal Sharma last updated on 09/Jun/20

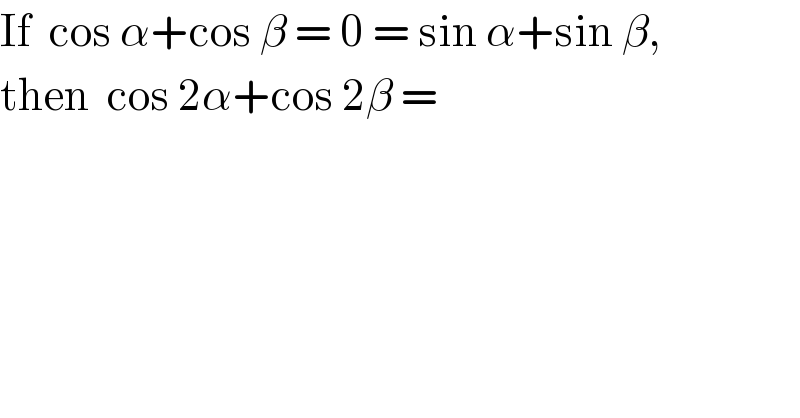
If cos α+cos β = 0 = sin α+sin β, then cos 2α+cos 2β =

$$\mathrm{If}\:\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta\:=\:\mathrm{0}\:=\:\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta, \\ $$$$\mathrm{then}\:\:\mathrm{cos}\:\mathrm{2}\alpha+\mathrm{cos}\:\mathrm{2}\beta\:= \\ $$

Commented by bemath last updated on 09/Jun/20

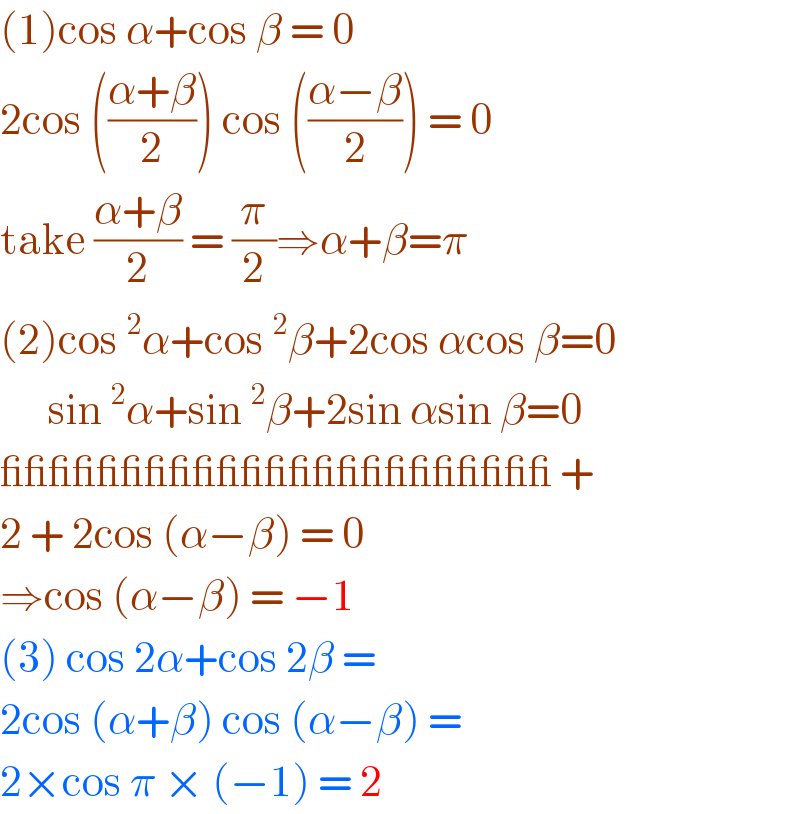
(1)cos α+cos β = 0 2cos (((α+β)/2)) cos (((α−β)/2)) = 0 take ((α+β)/2) = (π/2)⇒α+β=π (2)cos^2 α+cos^2 β+2cos αcos β=0 sin^2 α+sin^2 β+2sin αsin β=0 _______________________ + 2 + 2cos (α−β) = 0 ⇒cos (α−β) = −1 (3) cos 2α+cos 2β = 2cos (α+β) cos (α−β) = 2×cos π × (−1) = 2

$$\left(\mathrm{1}\right)\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta\:=\:\mathrm{0} \\ $$$$\mathrm{2cos}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\alpha−\beta}{\mathrm{2}}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{take}\:\frac{\alpha+\beta}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{2}}\Rightarrow\alpha+\beta=\pi \\ $$$$\left(\mathrm{2}\right)\mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{cos}\:^{\mathrm{2}} \beta+\mathrm{2cos}\:\alpha\mathrm{cos}\:\beta=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{sin}\:^{\mathrm{2}} \alpha+\mathrm{sin}\:^{\mathrm{2}} \beta+\mathrm{2sin}\:\alpha\mathrm{sin}\:\beta=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:+ \\ $$$$\mathrm{2}\:+\:\mathrm{2cos}\:\left(\alpha−\beta\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\left(\alpha−\beta\right)\:=\:−\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{cos}\:\mathrm{2}\alpha+\mathrm{cos}\:\mathrm{2}\beta\:= \\ $$$$\mathrm{2cos}\:\left(\alpha+\beta\right)\:\mathrm{cos}\:\left(\alpha−\beta\right)\:= \\ $$$$\mathrm{2}×\mathrm{cos}\:\pi\:×\:\left(−\mathrm{1}\right)\:=\:\mathrm{2} \\ $$

Facebook Tweet Pin

If-cos-cos-0-sin-sin-then-cos-2-cos-2-

Leave a Reply Cancel reply