Question Number 54034 by qw last updated on 28/Jan/19
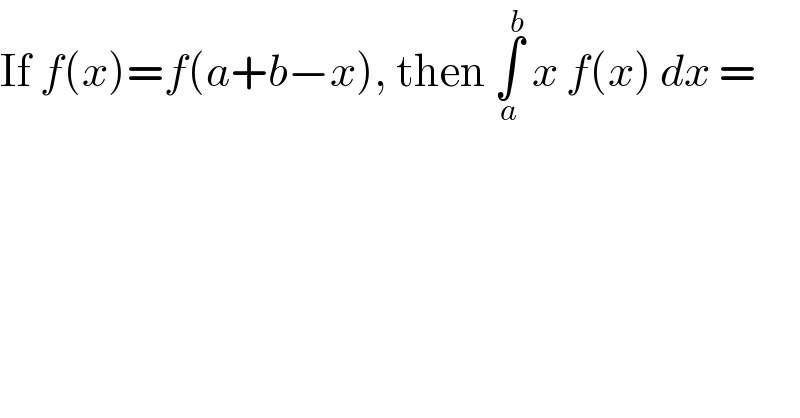
$$\mathrm{If}\:{f}\left({x}\right)={f}\left({a}+{b}−{x}\right),\:\mathrm{then}\:\underset{{a}} {\overset{{b}} {\int}}\:{x}\:{f}\left({x}\right)\:{dx}\:= \\ $$
Commented by maxmathsup by imad last updated on 28/Jan/19
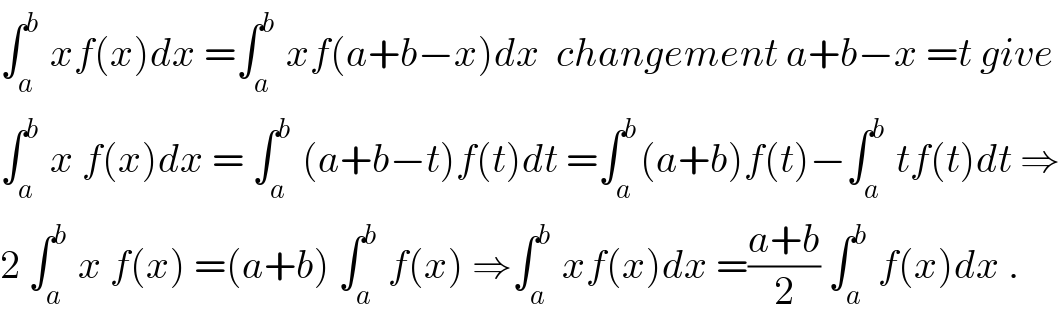
$$\int_{{a}} ^{{b}} \:{xf}\left({x}\right){dx}\:=\int_{{a}} ^{{b}} \:{xf}\left({a}+{b}−{x}\right){dx}\:\:{changement}\:{a}+{b}−{x}\:={t}\:{give} \\ $$$$\int_{{a}} ^{{b}} \:{x}\:{f}\left({x}\right){dx}\:=\:\int_{{a}} ^{{b}} \:\left({a}+{b}−{t}\right){f}\left({t}\right){dt}\:=\int_{{a}} ^{{b}} \left({a}+{b}\right){f}\left({t}\right)−\int_{{a}} ^{{b}} \:{tf}\left({t}\right){dt}\:\Rightarrow \\ $$$$\mathrm{2}\:\int_{{a}} ^{{b}} \:{x}\:{f}\left({x}\right)\:=\left({a}+{b}\right)\:\int_{{a}} ^{{b}} \:{f}\left({x}\right)\:\Rightarrow\int_{{a}} ^{{b}} \:{xf}\left({x}\right){dx}\:=\frac{{a}+{b}}{\mathrm{2}}\:\int_{{a}} ^{{b}} \:{f}\left({x}\right){dx}\:. \\ $$
