Menu Close

If-g-x-0-x-cos-4-t-dt-then-g-x-pi-

Tinku Tara 0 Comments
Pin




Question Number 30354 by soksan last updated on 21/Feb/18
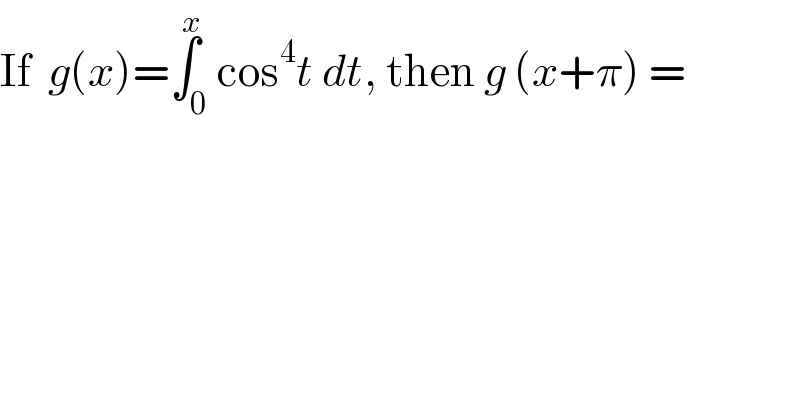
If g(x)=∫_0 ^x cos^4 t dt, then g (x+π) =
$$\mathrm{If}\:\:{g}\left({x}\right)=\overset{{x}} {\int}_{\mathrm{0}} \mathrm{cos}^{\mathrm{4}} {t}\:{dt},\:\mathrm{then}\:{g}\:\left({x}+\pi\right)\:= \\ $$
Answered by ajfour last updated on 21/Feb/18
g(x)=(1/4)∫_0 ^( x) (2cos^2 t)^2 dt =(1/4)∫_0 ^( x) (1+cos 2t)^2 dt =(1/4)∫_0 ^( x) (1+2cos 2t+cos^2 2t)dt =(x/4)+((sin 2x)/4)+(1/8)∫_0 ^( x) (1+cos 4t)dt =(x/4)+((sin 2x)/4)+(x/8)+((sin 4x)/(32)) g(x+π)= g(x)+((3π)/8) .
$${g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{2cos}\:^{\mathrm{2}} {t}\right)^{\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{t}\right)^{\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{1}+\mathrm{2cos}\:\mathrm{2}{t}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{t}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{{x}}{\mathrm{4}}+\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\:\:{x}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{t}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:=\frac{{x}}{\mathrm{4}}+\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}+\frac{{x}}{\mathrm{8}}+\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{32}} \\ $$$${g}\left({x}+\pi\right)=\:{g}\left({x}\right)+\frac{\mathrm{3}\pi}{\mathrm{8}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *