Question Number 9866 by richard last updated on 10/Jan/17
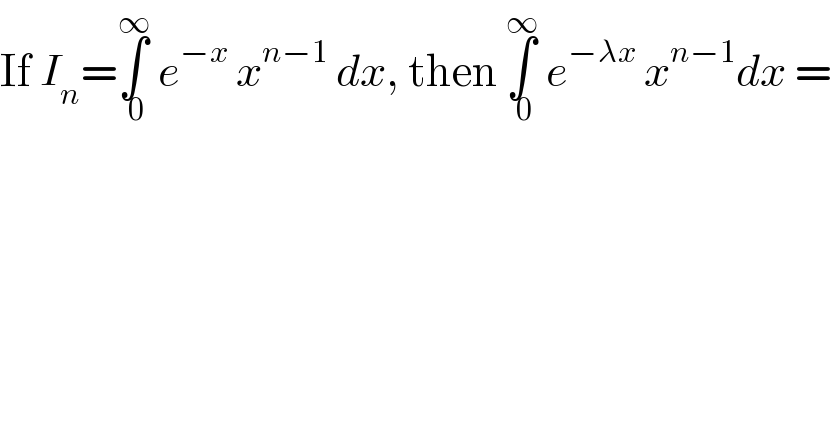
$$\mathrm{If}\:{I}_{{n}} =\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:{e}^{−{x}} \:{x}^{{n}−\mathrm{1}} \:{dx},\:\mathrm{then}\:\underset{\:\mathrm{0}} {\overset{\infty} {\int}}\:{e}^{−\lambda{x}} \:{x}^{{n}−\mathrm{1}} {dx}\:= \\ $$
