Question Number 113991 by deepraj123 last updated on 16/Sep/20
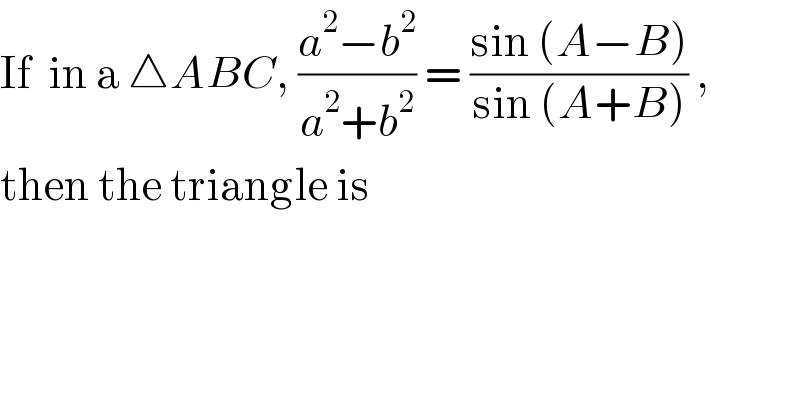
$$\mathrm{If}\:\:\mathrm{in}\:\mathrm{a}\:\bigtriangleup{ABC},\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{sin}\:\left({A}−{B}\right)}{\mathrm{sin}\:\left({A}+{B}\right)}\:, \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{is} \\ $$
Commented by som(math1967) last updated on 16/Sep/20
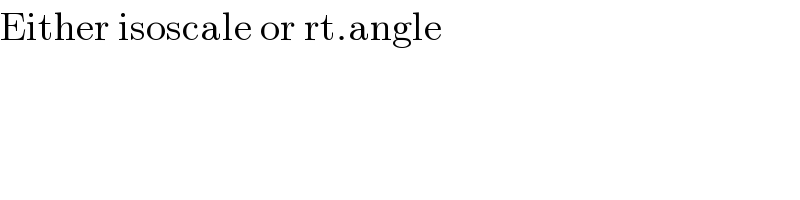
$$\mathrm{Either}\:\mathrm{isoscale}\:\mathrm{or}\:\mathrm{rt}.\mathrm{angle} \\ $$
Answered by 1549442205PVT last updated on 17/Sep/20

$$\mathrm{We}\:\mathrm{have}\:\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:\frac{\mathrm{sin}\:\left({A}−{B}\right)}{\mathrm{sin}\:\left({A}+{B}\right)} \\ $$$$\Leftrightarrow\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{sin}\left(\mathrm{A}−\mathrm{B}\right)}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{sin}\left(\mathrm{A}+\mathrm{B}\right)}=\frac{\mathrm{2a}^{\mathrm{2}} }{\mathrm{sin}\left(\mathrm{A}−\mathrm{B}\right)+\mathrm{sin}\left(\mathrm{A}+\mathrm{B}\right)}=\frac{\mathrm{2b}^{\mathrm{2}} }{\mathrm{sin}\left(\mathrm{A}+\mathrm{B}\right)−\mathrm{sin}\left(\mathrm{A}−\mathrm{B}\right)} \\ $$$$\Rightarrow\frac{\mathrm{2a}^{\mathrm{2}} }{\mathrm{2sinAcosB}}=\frac{\mathrm{2b}^{\mathrm{2}} }{\mathrm{2cosAsinB}}\left(\mathrm{1}\right) \\ $$$$\mathrm{From}\:\mathrm{sine}\:\mathrm{theorem}\:\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\frac{\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{A}}{\mathrm{sinAcosB}}=\frac{\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{B}}{\mathrm{sinBcosA}} \\ $$$$\Leftrightarrow\frac{\mathrm{sinA}}{\mathrm{cosB}}=\frac{\mathrm{sinB}}{\mathrm{cosA}}\Leftrightarrow\mathrm{2sinAcosA}=\mathrm{2sinBcosB} \\ $$$$\Leftrightarrow\mathrm{sin2A}=\mathrm{sin2B}\Leftrightarrow\mathrm{2A}=\mathrm{2B}\:\:\left(\mathrm{2}\right)\:\mathrm{or} \\ $$$$\mathrm{2A}=\mathrm{180}°−\mathrm{2B}\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\Leftrightarrow\mathrm{A}=\mathrm{B}\Leftrightarrow\Delta\mathrm{ABC}\:\mathrm{is}\:\mathrm{isosceles}\:\mathrm{at}\:\mathrm{C} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\mathrm{A}=\mathrm{90}°−\mathrm{B}\Leftrightarrow\Delta\mathrm{ABC}\:\mathrm{is}\:\mathrm{right}\:\mathrm{at}\:\mathrm{C} \\ $$
