Menu Close

If-sin-1-x-sin-1-1-x-cos-1-x-then-x-

Tinku Tara 0 Comments
Pin




Question Number 43643 by gunawan last updated on 13/Sep/18
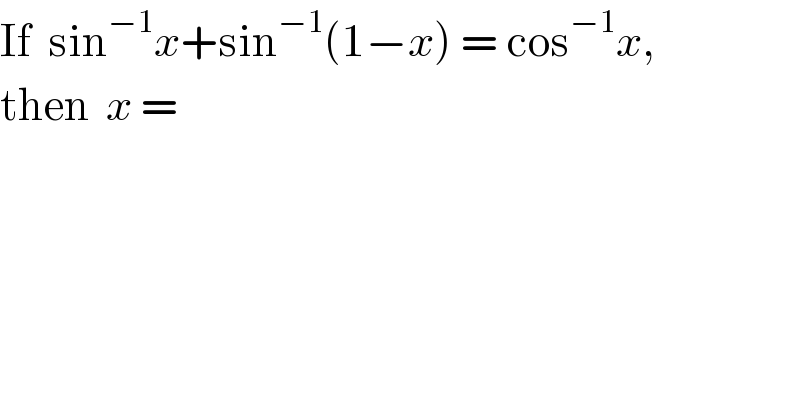
If sin^(−1) x+sin^(−1) (1−x) = cos^(−1) x, then x =
$$\mathrm{If}\:\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\:=\:\mathrm{cos}^{−\mathrm{1}} {x}, \\ $$$$\mathrm{then}\:\:{x}\:= \\ $$
Answered by behi83417@gmail.com last updated on 13/Sep/18
x=(1/2)
$${x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Sep/18
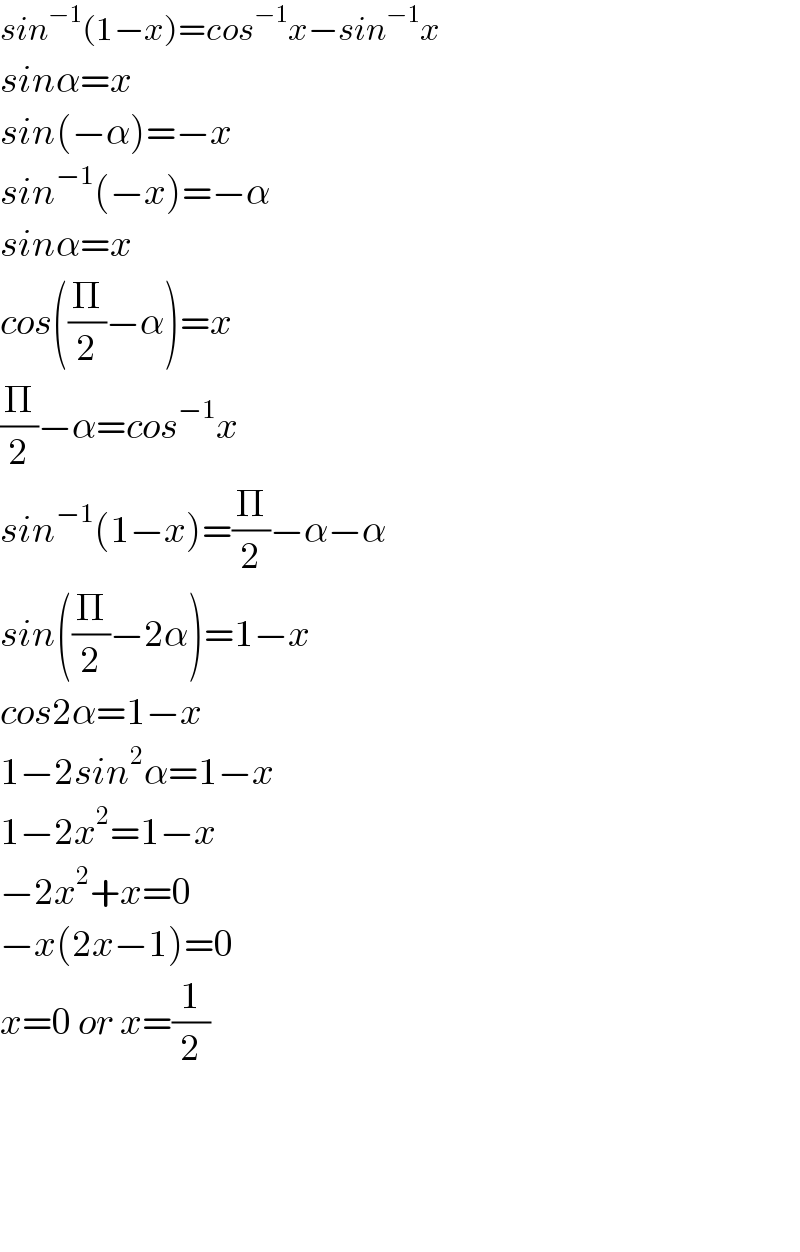
sin^(−1) (1−x)=cos^(−1) x−sin^(−1) x sinα=x sin(−α)=−x sin^(−1) (−x)=−α sinα=x cos((Π/2)−α)=x (Π/2)−α=cos^(−1) x sin^(−1) (1−x)=(Π/2)−α−α sin((Π/2)−2α)=1−x cos2α=1−x 1−2sin^2 α=1−x 1−2x^2 =1−x −2x^2 +x=0 −x(2x−1)=0 x=0 or x=(1/2)
$${sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)={cos}^{−\mathrm{1}} {x}−{sin}^{−\mathrm{1}} {x} \\ $$$${sin}\alpha={x} \\ $$$${sin}\left(−\alpha\right)=−{x} \\ $$$${sin}^{−\mathrm{1}} \left(−{x}\right)=−\alpha \\ $$$${sin}\alpha={x} \\ $$$${cos}\left(\frac{\Pi}{\mathrm{2}}−\alpha\right)={x} \\ $$$$\frac{\Pi}{\mathrm{2}}−\alpha={cos}^{−\mathrm{1}} {x} \\ $$$${sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)=\frac{\Pi}{\mathrm{2}}−\alpha−\alpha \\ $$$${sin}\left(\frac{\Pi}{\mathrm{2}}−\mathrm{2}\alpha\right)=\mathrm{1}−{x} \\ $$$${cos}\mathrm{2}\alpha=\mathrm{1}−{x} \\ $$$$\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \alpha=\mathrm{1}−{x} \\ $$$$\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$$−\mathrm{2}{x}^{\mathrm{2}} +{x}=\mathrm{0} \\ $$$$−{x}\left(\mathrm{2}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{or}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Joel578 last updated on 13/Sep/18
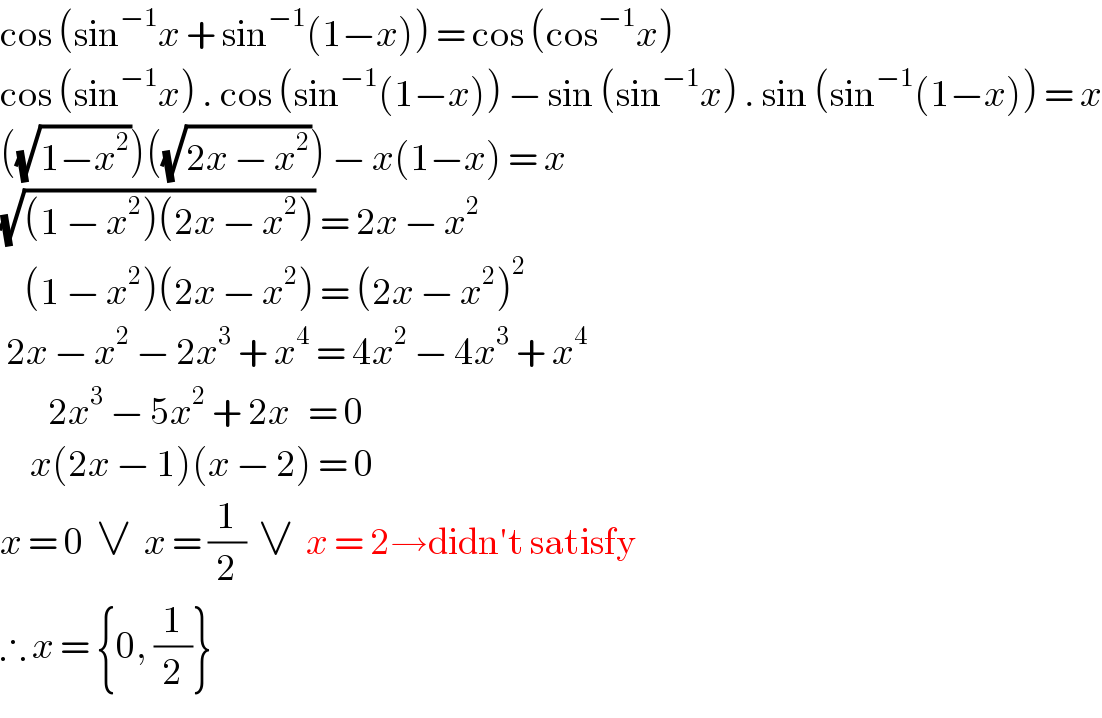
cos (sin^(−1) x + sin^(−1) (1−x)) = cos (cos^(−1) x) cos (sin^(−1) x) . cos (sin^(−1) (1−x)) − sin (sin^(−1) x) . sin (sin^(−1) (1−x)) = x ((√(1−x^2 )))((√(2x − x^2 ))) − x(1−x) = x (√((1 − x^2 )(2x − x^2 ))) = 2x − x^2 (1 − x^2 )(2x − x^2 ) = (2x − x^2 )^2 2x − x^2 − 2x^3 + x^4 = 4x^2 − 4x^3 + x^4 2x^3 − 5x^2 + 2x = 0 x(2x − 1)(x − 2) = 0 x = 0 ∨ x = (1/2) ∨ x = 2→didn′t satisfy ∴ x = {0, (1/2)}
$$\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\:+\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)\:=\:\mathrm{cos}\:\left(\mathrm{cos}^{−\mathrm{1}} {x}\right) \\ $$$$\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\:.\:\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)\:−\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)\:.\:\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)\right)\:=\:{x} \\ $$$$\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\left(\sqrt{\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} }\right)\:−\:{x}\left(\mathrm{1}−{x}\right)\:=\:{x} \\ $$$$\sqrt{\left(\mathrm{1}\:−\:{x}^{\mathrm{2}} \right)\left(\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} \right)}\:=\:\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} \\ $$$$\:\:\:\:\left(\mathrm{1}\:−\:{x}^{\mathrm{2}} \right)\left(\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} \right)\:=\:\left(\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\mathrm{2}{x}\:−\:{x}^{\mathrm{2}} \:−\:\mathrm{2}{x}^{\mathrm{3}} \:+\:{x}^{\mathrm{4}} \:=\:\mathrm{4}{x}^{\mathrm{2}} \:−\:\mathrm{4}{x}^{\mathrm{3}} \:+\:{x}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{3}} \:−\:\mathrm{5}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:\:\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:{x}\left(\mathrm{2}{x}\:−\:\mathrm{1}\right)\left({x}\:−\:\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{0}\:\:\vee\:\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\vee\:\:{x}\:=\:\mathrm{2}\rightarrow\mathrm{didn}'\mathrm{t}\:\mathrm{satisfy} \\ $$$$\therefore\:{x}\:=\:\left\{\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$
Commented by gunawan last updated on 13/Sep/18
Nice thank you very much Sir
$$\mathrm{Nice}\: \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *