Question Number 53924 by F_Nongue last updated on 27/Jan/19
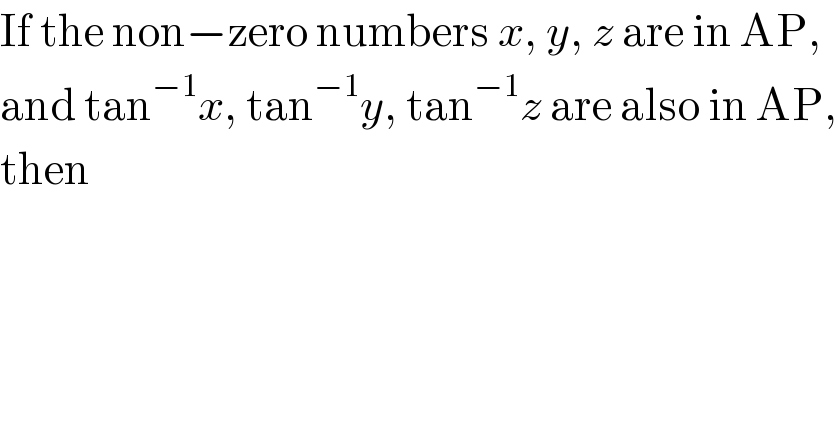
$$\mathrm{If}\:\mathrm{the}\:\mathrm{non}−\mathrm{zero}\:\mathrm{numbers}\:{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP}, \\ $$$$\mathrm{and}\:\mathrm{tan}^{−\mathrm{1}} {x},\:\mathrm{tan}^{−\mathrm{1}} {y},\:\mathrm{tan}^{−\mathrm{1}} {z}\:\mathrm{are}\:\mathrm{also}\:\mathrm{in}\:\mathrm{AP}, \\ $$$$\mathrm{then} \\ $$
Answered by $@ty@m last updated on 27/Jan/19
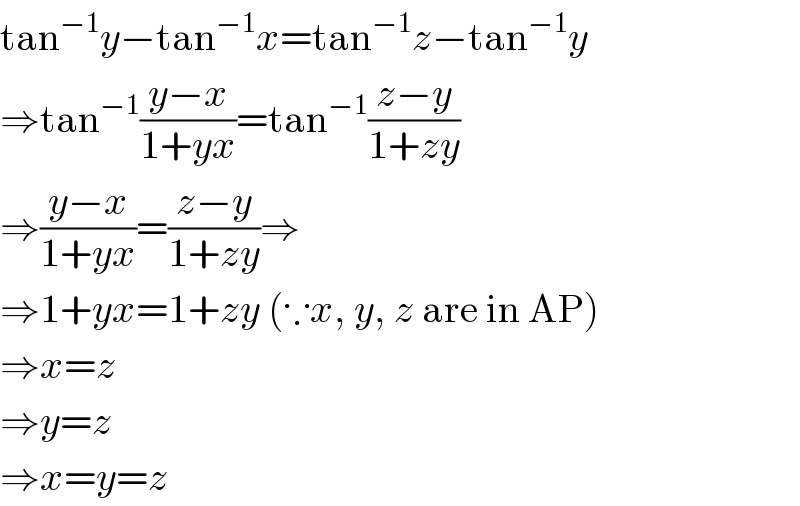
$$\mathrm{tan}^{−\mathrm{1}} {y}−\mathrm{tan}^{−\mathrm{1}} {x}=\mathrm{tan}^{−\mathrm{1}} {z}−\mathrm{tan}^{−\mathrm{1}} {y} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \frac{{y}−{x}}{\mathrm{1}+{yx}}=\mathrm{tan}^{−\mathrm{1}} \frac{{z}−{y}}{\mathrm{1}+{zy}} \\ $$$$\Rightarrow\frac{{y}−{x}}{\mathrm{1}+{yx}}=\frac{{z}−{y}}{\mathrm{1}+{zy}}\Rightarrow \\ $$$$\Rightarrow\mathrm{1}+{yx}=\mathrm{1}+{zy}\:\left(\because{x},\:{y},\:{z}\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP}\right) \\ $$$$\Rightarrow{x}={z} \\ $$$$\Rightarrow{y}={z} \\ $$$$\Rightarrow{x}={y}={z} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jan/19

$${given}\:\mathrm{2}{y}={x}+{z} \\ $$$$\mathrm{2}{tan}^{−\mathrm{1}} {y}={tan}^{−\mathrm{1}} {x}+{tan}^{−\mathrm{1}} {z} \\ $$$${tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{y}}{\mathrm{1}−{y}^{\mathrm{2}} }\right)={tan}^{−\mathrm{1}} \left(\frac{{x}+{z}}{\mathrm{1}−{xz}}\right) \\ $$$$\frac{\mathrm{2}{y}}{\mathrm{1}−{y}^{\mathrm{2}} }=\frac{{x}+{z}}{\mathrm{1}−{xz}} \\ $$$$\mathrm{2}{y}−\mathrm{2}{xyz}={x}+{z}−{xy}^{\mathrm{2}} −{zy}^{\mathrm{2}} \\ $$$${xy}^{\mathrm{2}} +{zy}^{\mathrm{2}} −\mathrm{2}{xyz}=\mathrm{0} \\ $$$${xy}+{zy}−\mathrm{2}{xz}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{{x}}=\frac{\mathrm{2}}{{y}} \\ $$$${x},{y}\:{and}\:{z}\:{in}\:{H}.{P}\:{also}… \\ $$$${Peculiar}\:{conclusion}… \\ $$$${pls}\:{clearly}\:{mention}\:{in}\:{question}\:{what}\:{to}\:{prove}… \\ $$$$ \\ $$
