Question Number 35534 by jonesme last updated on 20/May/18
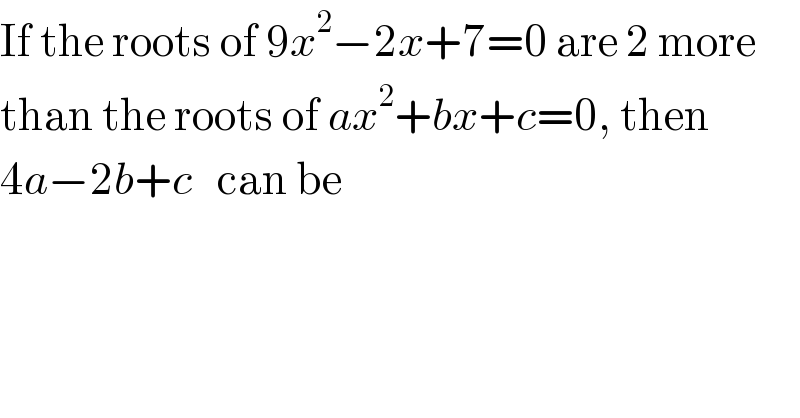
$$\mathrm{If}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{7}=\mathrm{0}\:\mathrm{are}\:\mathrm{2}\:\mathrm{more} \\ $$$$\mathrm{than}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0},\:\mathrm{then} \\ $$$$\mathrm{4}{a}−\mathrm{2}{b}+{c}\:\:\:\mathrm{can}\:\mathrm{be} \\ $$
Answered by ajfour last updated on 20/May/18
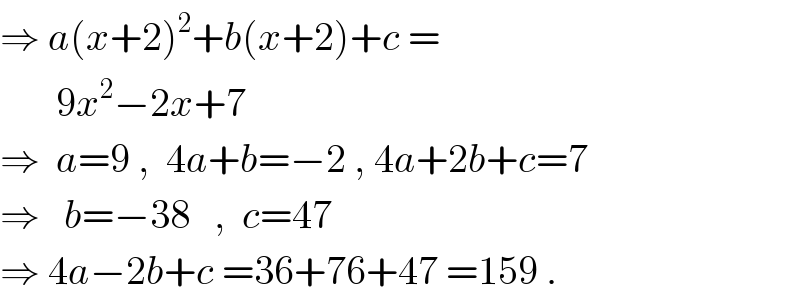
$$\Rightarrow\:{a}\left({x}+\mathrm{2}\right)^{\mathrm{2}} +{b}\left({x}+\mathrm{2}\right)+{c}\:= \\ $$$$\:\:\:\:\:\:\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{7} \\ $$$$\Rightarrow\:\:{a}=\mathrm{9}\:,\:\:\mathrm{4}{a}+{b}=−\mathrm{2}\:,\:\mathrm{4}{a}+\mathrm{2}{b}+{c}=\mathrm{7} \\ $$$$\Rightarrow\:\:\:{b}=−\mathrm{38}\:\:\:,\:\:{c}=\mathrm{47} \\ $$$$\Rightarrow\:\mathrm{4}{a}−\mathrm{2}{b}+{c}\:=\mathrm{36}+\mathrm{76}+\mathrm{47}\:=\mathrm{159}\:. \\ $$
