If-the-roots-of-the-equation-ax-2-bx-5c-0-are-in-the-ratio-of-4-5-then-4b-2-81ac-

Question Number 30183 by Surajitzzz last updated on 17/Feb/18

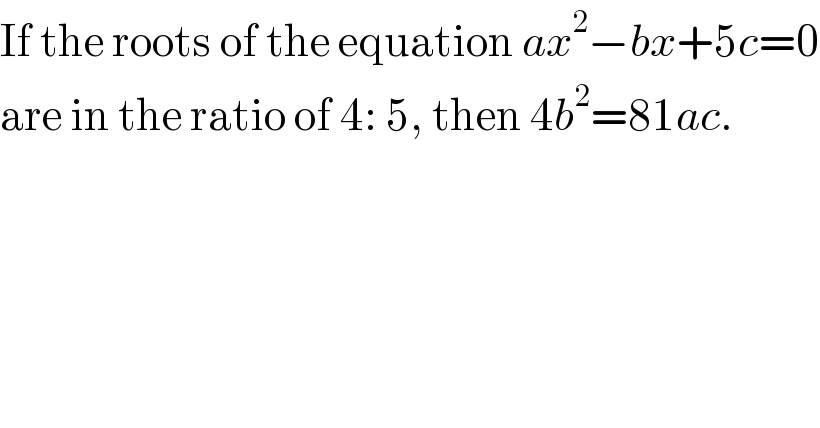
If the roots of the equation {a x}^{2} - b x + 5 c = 0

are in the ratio of 4 : 5, then 4 b^{2} = 81 a c .

Answered by Rasheed.Sindhi last updated on 18/Feb/18

Let the roots are 4 k & 5 k

Sum of the roots = \frac{b}{a} = (4 + 5) k = 9 k

\Rightarrow k = \frac{b}{9 a}

Product of the roots = \frac{5 c}{a} = (4 k) (5 k) = {20 k}^{2}

= 20 {(\frac{b}{9 a})}^{2} = \frac{{20 b}^{2}}{{81 a}^{2}}

\frac{5 c}{a} = \frac{{20 b}^{2}}{{81 a}^{2}}

c = \frac{{4 b}^{2}}{81 a}

{4 b}^{2} = 81 ac