Question Number 43630 by peter frank last updated on 12/Sep/18
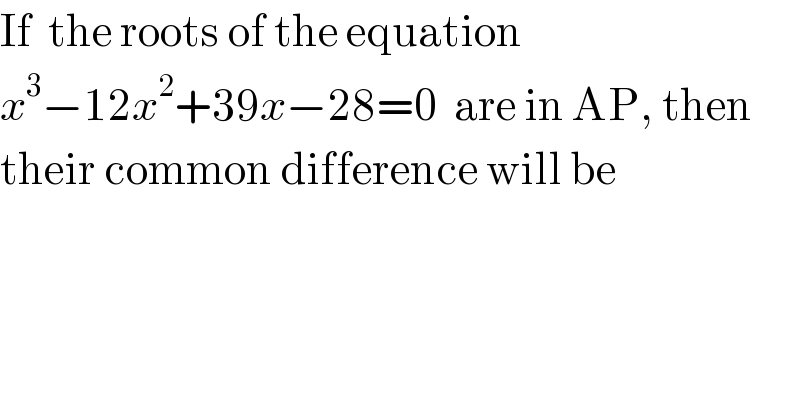
$$\mathrm{If}\:\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$${x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} +\mathrm{39}{x}−\mathrm{28}=\mathrm{0}\:\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP},\:\mathrm{then} \\ $$$$\mathrm{their}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{will}\:\mathrm{be} \\ $$
Answered by $@ty@m last updated on 13/Sep/18

$$\left(\alpha−\beta\right)+\alpha+\left(\alpha+\beta\right)=\mathrm{12} \\ $$$$\Rightarrow\mathrm{3}\alpha=\mathrm{12} \\ $$$$\Rightarrow\alpha=\mathrm{4}\:…\left(\mathrm{1}\right) \\ $$$$\left(\alpha−\beta\right).\alpha.\left(\alpha+\beta\right)=\mathrm{28} \\ $$$$\Rightarrow\alpha.\left(\alpha^{\mathrm{2}} −\beta^{\mathrm{2}} \right)=\mathrm{28} \\ $$$$\Rightarrow\mathrm{4}×\left(\mathrm{4}^{\mathrm{2}} −\beta^{\mathrm{2}} \right)=\mathrm{28} \\ $$$$\Rightarrow\mathrm{16}−\beta^{\mathrm{2}} =\mathrm{7} \\ $$$$\Rightarrow\beta^{\mathrm{2}} =\mathrm{9} \\ $$$$\beta=\pm\mathrm{3}\:{Ans}. \\ $$
