If-the-roots-of-the-quadratic-equation-x-2-px-q-0-are-tan-30-and-tan-15-respectively-then-the-value-of-2-q-p-is-

Question Number 9722 by supungamage001 last updated on 29/Dec/16

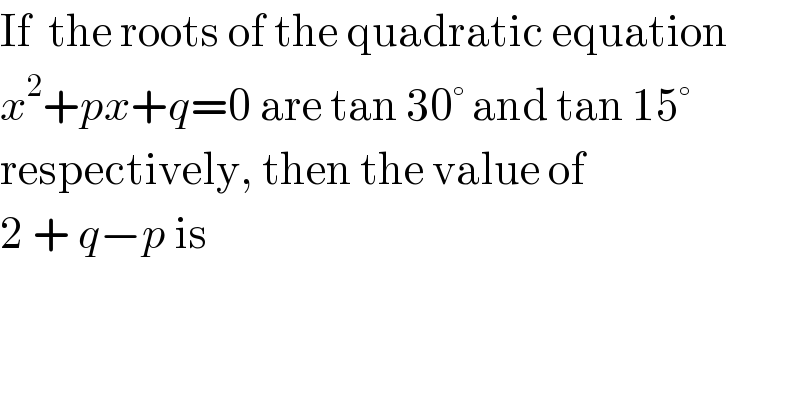
If the roots of the quadratic equation

x^{2} + p x + q = 0 are \tan 30 ° and \tan 15 °

respectively, then the value of

2 + q - p is

Commented by ridwan balatif last updated on 29/Dec/16

{\tan 30}^{o} = \frac{1}{3} \sqrt{3}

{\tan 15}^{o} = \tan (45 - 30)

= \frac{{\tan 45}^{o} - {\tan 30}^{o}}{1 + {\tan 45}^{o} \times {\tan 30}^{o}}

= \frac{1 - \frac{1}{3} \sqrt{3}}{1 + \frac{1}{3} \sqrt{3}}

= \frac{3 - \sqrt{3}}{3 + \sqrt{3}} \times (\frac{3 - \sqrt{3}}{3 - \sqrt{3}})

= \frac{12 - 6 \sqrt{3}}{6}

= 2 - \sqrt{3}

as we know {\tan 30}^{o} and {\tan 15}^{0} is the root of the equation x^{2} + px + q = 0

(x - {\tan 30}^{o}) (x - {\tan 15}^{o}) = 0

(x - \frac{1}{3} \sqrt{3}) (x - (2 - \sqrt{3})) = 0

x^{2} - (\frac{1}{3} \sqrt{3} + 2 - \sqrt{3}) x + \frac{1}{3} \sqrt{3} (2 - \sqrt{3}) = 0

x^{2} - (- \frac{2}{3} \sqrt{3} + 2) x + \frac{2}{3} \sqrt{3} - 1 = 0

x^{2} + px + q = 0

p = - 2 + \frac{2}{3} \sqrt{3} q = \frac{2}{3} \sqrt{3} - 1

2 + q - p = 2 + \frac{2}{3} \sqrt{3} - 1 + 2 - \frac{2}{3} \sqrt{3}

= 3

Commented by ridwan balatif last updated on 30/Dec/16

kita tau bahwa {\tan 30}^{o} dan \tan 15^{o} adalah suatu

akar akar dari suatu persamaan kuadrat, maka

(x - {\tan 15}^{o}) (x - {\tan 30}^{o}) = 0

x^{2} - ({\tan 30}^{o} + {\tan 15}^{o}) x + {\tan 30}^{o} \times {\tan 15}^{o} = 0

x^{2} + px + q = 0

gunakan kesamaan matematika, kita dapati

- p = {\tan 30}^{o} + {\tan 15}^{o}

q = {\tan 30}^{o} \times {\tan 15}^{o}

kita tau bahwa

{\tan 45}^{o} = \tan (30^{o} + 15^{o})

1 = \frac{{\tan 30}^{o} + {\tan 15}^{o}}{1 - {\tan 30}^{o} \times {\tan 15}^{o}}

1 = \frac{- p}{1 - q}

1 - q = - p

q - p = 1

jadi, 2 + (q - p) = 2 + 1 = 3

Commented by Joel575 last updated on 31/Dec/16

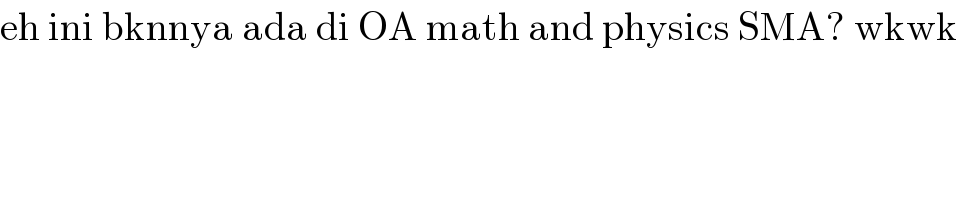
eh ini bknnya ada di OA math and physics SMA ? wkwk

Commented by ridwan balatif last updated on 31/Dec/16

memang ada