Question Number 24459 by mustafasediqi last updated on 18/Nov/17
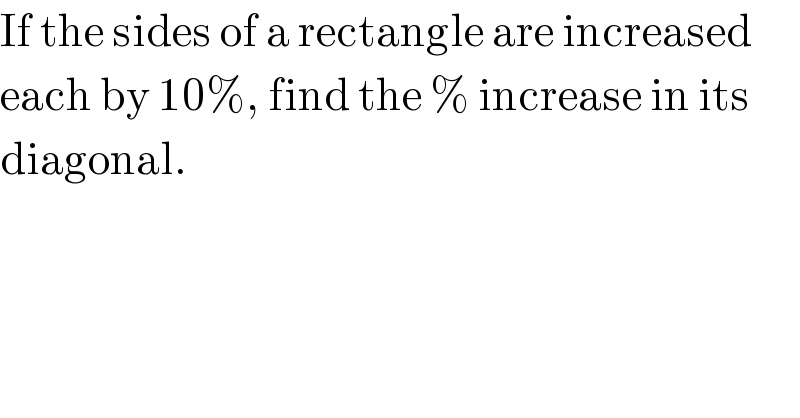
$$\mathrm{If}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{rectangle}\:\mathrm{are}\:\mathrm{increased} \\ $$$$\mathrm{each}\:\mathrm{by}\:\mathrm{10\%},\:\mathrm{find}\:\mathrm{the}\:\%\:\mathrm{increase}\:\mathrm{in}\:\mathrm{its} \\ $$$$\mathrm{diagonal}. \\ $$
Answered by ajfour last updated on 18/Nov/17
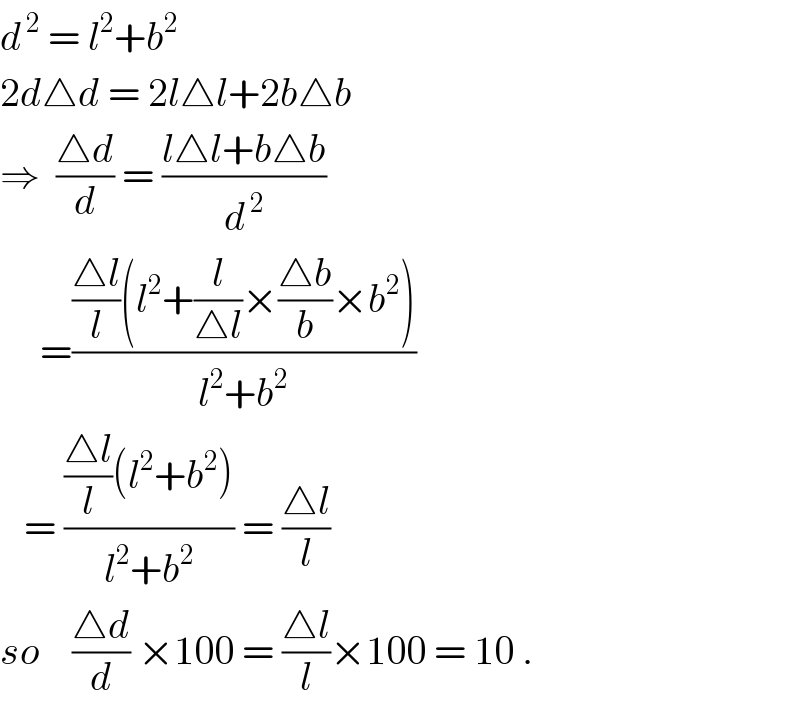
$${d}^{\:\mathrm{2}} \:=\:{l}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\mathrm{2}{d}\bigtriangleup{d}\:=\:\mathrm{2}{l}\bigtriangleup{l}+\mathrm{2}{b}\bigtriangleup{b} \\ $$$$\Rightarrow\:\:\frac{\bigtriangleup{d}}{{d}}\:=\:\frac{{l}\bigtriangleup{l}+{b}\bigtriangleup{b}}{{d}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:=\frac{\frac{\bigtriangleup{l}}{{l}}\left({l}^{\mathrm{2}} +\frac{{l}}{\bigtriangleup{l}}×\frac{\bigtriangleup{b}}{{b}}×{b}^{\mathrm{2}} \right)}{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{\frac{\bigtriangleup{l}}{{l}}\left({l}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:\frac{\bigtriangleup{l}}{{l}} \\ $$$${so}\:\:\:\:\frac{\bigtriangleup{d}}{{d}}\:×\mathrm{100}\:=\:\frac{\bigtriangleup{l}}{{l}}×\mathrm{100}\:=\:\mathrm{10}\:. \\ $$
Answered by $@ty@m last updated on 18/Nov/17

$${New}\:{diagonal}=\sqrt{\left(\frac{\mathrm{110}}{\mathrm{100}}{l}\right)^{\mathrm{2}} +\left(\frac{\mathrm{110}}{\mathrm{100}}{b}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{110}}{\mathrm{100}}\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${increase}=\left(\frac{\mathrm{110}}{\mathrm{100}}−\mathrm{1}\right)\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{10}}{\mathrm{100}}\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\%\:{increase}=\frac{\frac{\mathrm{10}}{\mathrm{100}}\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\:\sqrt{{l}^{\mathrm{2}} +{b}^{\mathrm{2}} }}×\mathrm{100} \\ $$$$=\mathrm{10} \\ $$$$\Rightarrow\mathrm{10\%}\:{increase} \\ $$
