Question Number 44315 by Tip Top last updated on 26/Sep/18

$$\mathrm{If}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{coefficients}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{2}{x}\right)^{{n}} \:\mathrm{is}\:\mathrm{6561},\:\mathrm{then}\:\mathrm{the} \\ $$$$\mathrm{greatest}\:\mathrm{coefficient}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{is} \\ $$
Answered by MrW3 last updated on 27/Sep/18
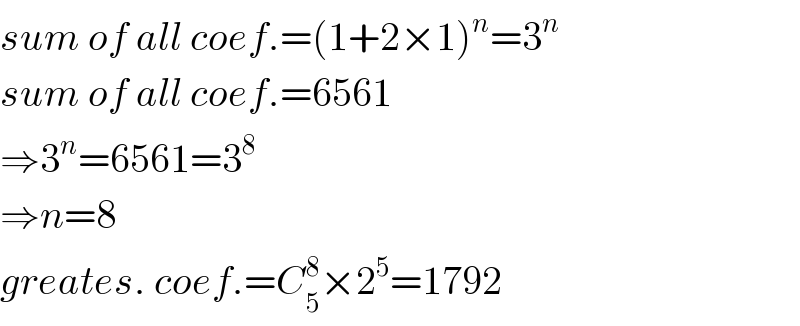
$${sum}\:{of}\:{all}\:{coef}.=\left(\mathrm{1}+\mathrm{2}×\mathrm{1}\right)^{{n}} =\mathrm{3}^{{n}} \\ $$$${sum}\:{of}\:{all}\:{coef}.=\mathrm{6561} \\ $$$$\Rightarrow\mathrm{3}^{{n}} =\mathrm{6561}=\mathrm{3}^{\mathrm{8}} \\ $$$$\Rightarrow{n}=\mathrm{8} \\ $$$${greates}.\:{coef}.={C}_{\mathrm{5}} ^{\mathrm{8}} ×\mathrm{2}^{\mathrm{5}} =\mathrm{1792} \\ $$
