Question Number 26712 by julli deswal last updated on 28/Dec/17
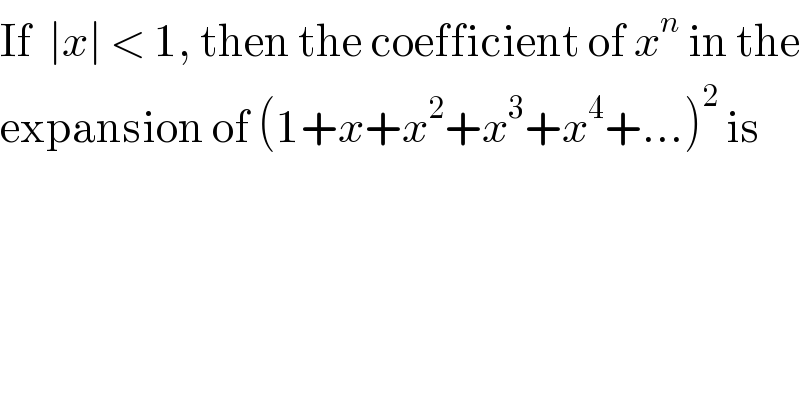
$$\mathrm{If}\:\:\mid{x}\mid\:<\:\mathrm{1},\:\mathrm{then}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{n}} \:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +…\right)^{\mathrm{2}} \:\mathrm{is} \\ $$
Answered by mrW1 last updated on 28/Dec/17
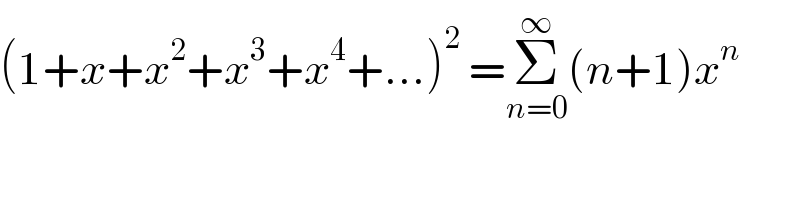
$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +…\right)^{\mathrm{2}} \:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \\ $$
