If-x-y-z-are-in-GP-and-x-3-y-3-z-3-are-in-HP-then-

Question Number 30156 by naybr last updated on 17/Feb/18

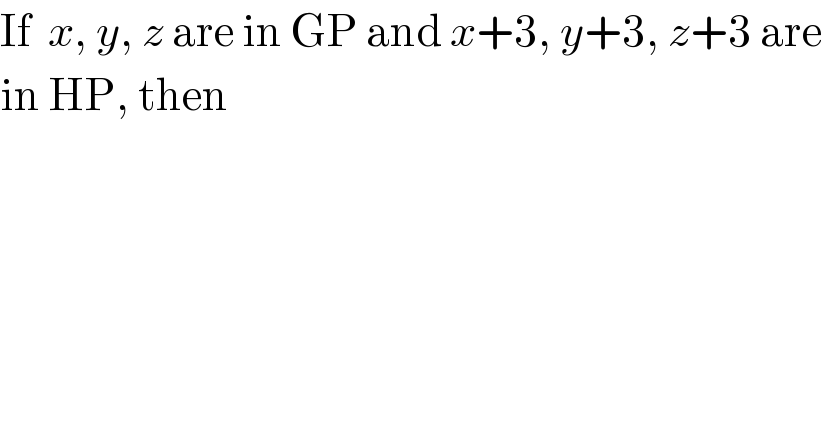
If x, y, z are in GP and x + 3, y + 3, z + 3 are

in HP, then

Answered by ajfour last updated on 17/Feb/18

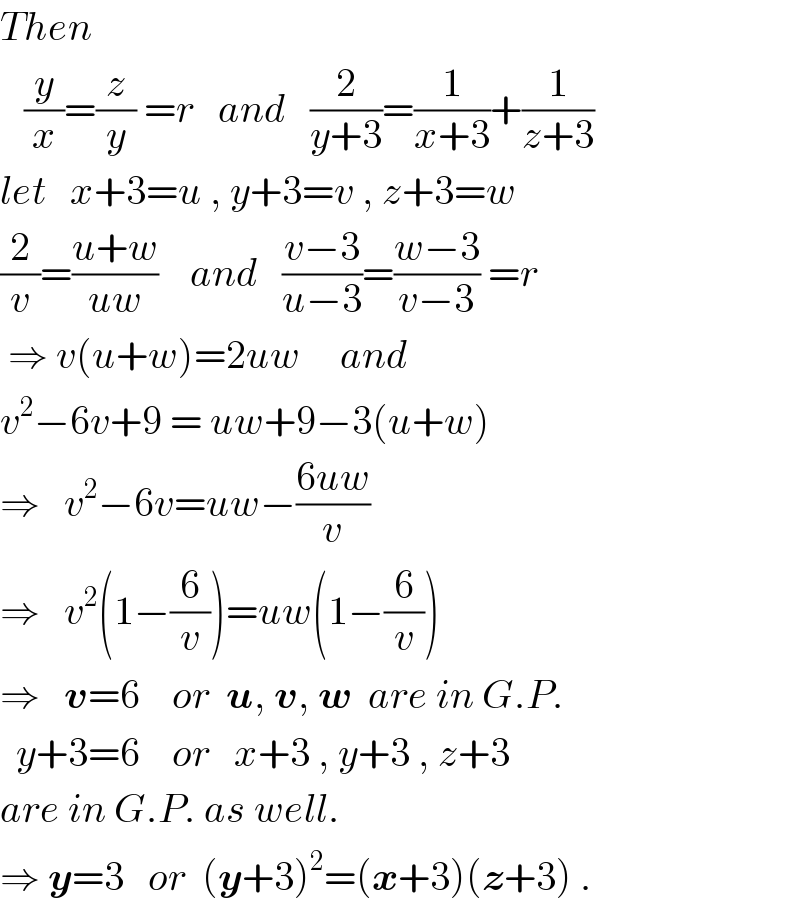
T h e n

\frac{y}{x} = \frac{z}{y} = r a n d \frac{2}{y + 3} = \frac{1}{x + 3} + \frac{1}{z + 3}

l e t x + 3 = u, y + 3 = v, z + 3 = w

\frac{2}{v} = \frac{u + w}{u w} a n d \frac{v - 3}{u - 3} = \frac{w - 3}{v - 3} = r

\Rightarrow v (u + w) = 2 u w a n d

v^{2} - 6 v + 9 = u w + 9 - 3 (u + w)

\Rightarrow v^{2} - 6 v = u w - \frac{6 u w}{v}

\Rightarrow v^{2} (1 - \frac{6}{v}) = u w (1 - \frac{6}{v})

\Rightarrow v = 6 o r u, v, w a r e i n G . P .

y + 3 = 6 o r x + 3, y + 3, z + 3

a r e i n G . P . a s w e l l .

\Rightarrow y = 3 o r {(y + 3)}^{2} = (x + 3) (z + 3) .

Facebook Tweet Pin